Open In App

Lasso vs Ridge vs Elastic Net | ML

Last Updated : 10 Jan, 2023
Improve
Improve
Like Article
Like
Save
Share
Report
Bias: Biases are the underlying assumptions that are made by data to simplify the target function. Bias does help us generalize the data better and make the model less sensitive to single data points. It also decreases the training time because of the decrease in complexity of target function High bias suggest that there is more assumption taken on target function. This leads to the underfitting of the model sometimes. Examples of High bias Algorithms include Linear Regression, Logistic Regression etc. Variance: In machine learning, Variance is a type of error that occurs due to a model’s sensitivity to small fluctuations in the dataset. The high variance would cause an algorithm to model the outliers/noise in the training set. This is most commonly referred to as overfitting. In this situation, the model basically learns every data point and does not offer good prediction when it tested on a novel dataset. Examples of High variance Algorithms include Decision Tree, KNN etc.

Overfitting vs Underfitting vs Just Right

Error in Linear Regression : Let’s consider a simple regression model that aims to predict a variable Y, from the linear combination of variables X and a normally distributed error term \epsilon
Y = \beta * X + \epsilon
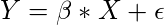
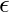
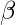
where \epsilon is the normal distribution that adds some noise in the prediction. Here \beta is the vector representing the coefficient of variables in the X that we need to estimate from the training data. We need to estimate them in such a way that it produces the lowest residual error. This error is defined as:
L_{ols}({\hat{\beta}})= \sum_{i=0}^{n} \left \| y_{i} - x_{i} * \hat{\beta_{i}} \right \|^2 = \left \| Y - X * \hat{\beta} \right \|^{2}
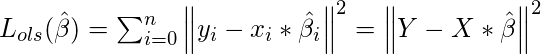
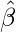
To calculate \hat{\beta} we use the following matrix transformation.
\hat{\beta_{ols}} = \left ( X^{T}X \right )^{-1}\left ( X^{T}Y \right )
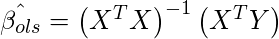
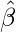
Here Bias and Variance of \hat{\beta} can be defined as:
Bias(hat{\beta}) = E\left ( \hat{\beta} \right ) - \beta
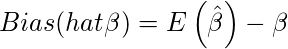
and
Variance\left ( \hat{\beta} \right ) =\sigma ^{2}\left ( {X}'X \right )^{-1}
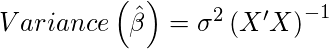
We can simplify the error term of the OLS equation defined above in terms of bias and variance as follows:
Error-term = \left ( E\left ( X\hat{\beta} \right ) - X\beta \right )^{2} +E\left ( X\hat{\beta} - E\left ( X\hat{\beta} \right ) \right )^{2}+\sigma^{2}
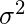
The first term of above equation represents Bias2. The second term represents Variance and the third term (\sigma^{2}) is unreducible error term.
Variance/ Bias vs Error

Variance/ Bias vs Error

Bias vs Variance Tradeoff
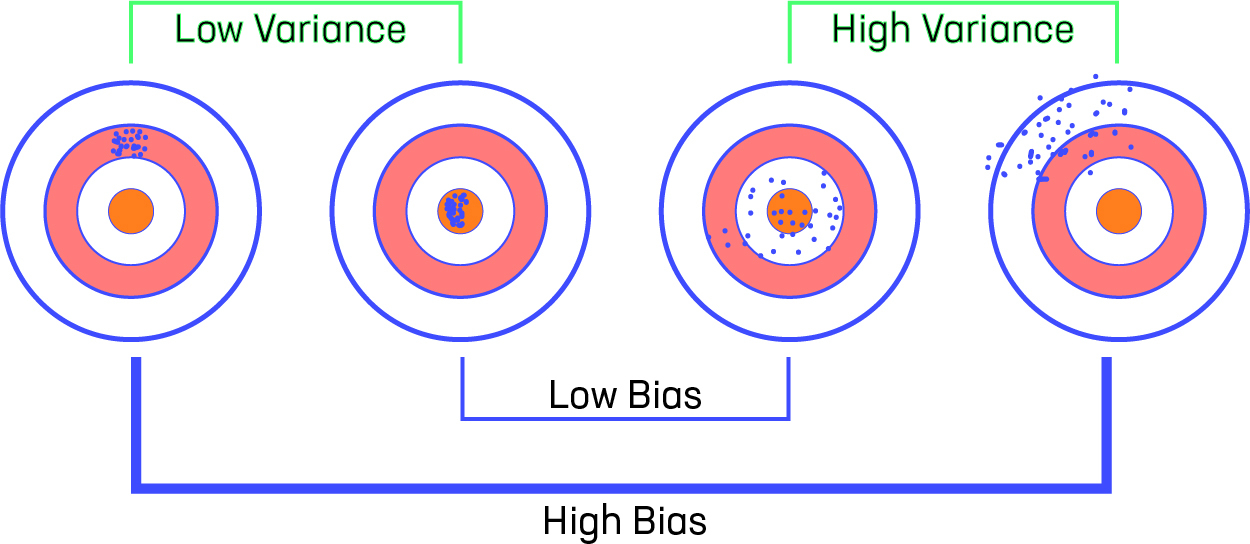
Variance-Bias-Visualization

Variance-Bias-Visualization

Let us consider that we have a very accurate model, this model has a low error in predictions and it’s not from the target (which is represented by bull’s eye). This model has low bias and variance. Now, if the predictions are scattered here and there then that is the symbol of high variance, also if the predictions are far from the target then that is the symbol of high bias. Sometimes we need to choose between low variance and low bias. There is an approach that prefers some bias over high variance, this approach is called Regularization. It works well for most of the classification/regression problems. Ridge Regression : In Ridge regression, we add a penalty term which is equal to the square of the coefficient. The L2 term is equal to the square of the magnitude of the coefficients. 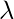We also add a coefficient \lambda to control that penalty term. 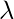In this case if \lambda is zero then the equation is the basic OLS else if \lambda \, > \, 0 then it will add a constraint to the coefficient. 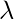As we increase the value of \lambda this constraint causes the value of the coefficient to tend towards zero. This leads to tradeoff of higher bias (dependencies on certain coefficients tend to be 0 and on certain coefficients tend to be very large, making the model less flexible) for lower variance.
L_{ridge} = argmin_{\hat{\beta}}\left ({\left \| Y- \beta * X \right \|}^{2} + \lambda * {\left \| \beta \right \|}_{2}^{2} \right )
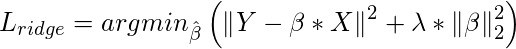
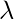
where \lambda is regularization penalty. Limitation of Ridge Regression: Ridge regression decreases the complexity of a model but does not reduce the number of variables since it never leads to a coefficient been zero rather only minimizes it. Hence, this model is not good for feature reduction. Lasso Regression : Lasso regression stands for Least Absolute Shrinkage and Selection Operator. It adds penalty term to the cost function. This term is the absolute sum of the coefficients. As the value of coefficients increases from 0 this term penalizes, cause model, to decrease the value of coefficients in order to reduce loss. The difference between ridge and lasso regression is that it tends to make coefficients to absolute zero as compared to Ridge which never sets the value of coefficient to absolute zero.
L_{lasso} = argmin_{\hat{\beta}}\left ({\left \| Y- \beta * X \right \|}^{2} + \lambda * {\left \| \beta \right \|}_{1} \right )
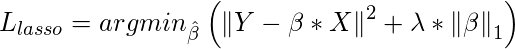Limitation of Lasso Regression:
  • Lasso sometimes struggles with some types of data. If the number of predictors (p) is greater than the number of observations (n), Lasso will pick at most n predictors as non-zero, even if all predictors are relevant (or may be used in the test set).
  • If there are two or more highly collinear variables then LASSO regression select one of them randomly which is not good for the interpretation of data
Elastic Net : Sometimes, the lasso regression can cause a small bias in the model where the prediction is too dependent upon a particular variable. In these cases, elastic Net is proved to better it combines the regularization of both lasso and Ridge. The advantage of that it does not easily eliminate the high collinearity coefficient.
L_{elasticNet} = argmin_{\hat{\beta}}\left ( \hat\beta \right )\left ( \sum \left ( y - x_i^J\hat{\beta} \right )^2 \right )/2n + \lambda \left ( (1 -\alpha )/2 * \sum_{j=1}^{m} \hat{\beta_{j}^{2}} + \alpha * \sum_{j=1}^{m} \left \| \hat{\beta_{j}} \right \| \right)
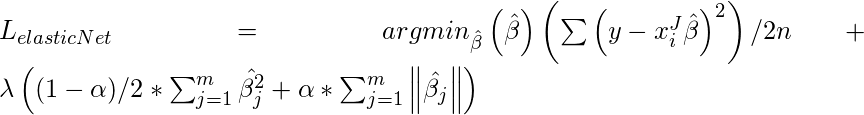  Reference – Elastic Net Paper

P
pawangfg
Improve
Next Article
Implementation of Lasso, Ridge and Elastic Net

Similar Reads

Implementation of Lasso, Ridge and Elastic Net
In this article, we will look into the implementation of different regularization techniques. First, we will start with multiple linear regression. For that, we require the python3 environment with sci-kit learn and pandas preinstall. We can also use google collaboratory or any other jupyter notebook environment.First, we need to import some packag
7 min read
Elastic Net Regression in R Programming
Elastic Net regression is a classification algorithm that overcomes the limitations of the lasso(least absolute shrinkage and selection operator) method which uses a penalty function in its L1 regularization. Elastic Net regression is a hybrid approach that blends both penalizations of the L2 and L1 regularization of lasso and ridge methods. It fin
3 min read
Implementation of Elastic Net Regression From Scratch
Prerequisites: Linear RegressionGradient DescentLasso & Ridge RegressionIntroduction: Elastic-Net Regression is a modification of Linear Regression which shares the same hypothetical function for prediction. The cost function of Linear Regression is represented by J. [Tex]\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)}-h\left(x^{(i)}\right)\right)^{2}[
5 min read
ML | Ridge Regressor using sklearn
A Ridge regressor is basically a regularized version of a Linear Regressor. i.e to the original cost function of linear regressor we add a regularized term that forces the learning algorithm to fit the data and helps to keep the weights lower as possible. The regularized term has the parameter 'alpha' which controls the regularization of the model
3 min read
Implementation of Ridge Regression from Scratch using Python
Prerequisites: Linear Regression Gradient Descent Introduction: Ridge Regression ( or L2 Regularization ) is a variation of Linear Regression. In Linear Regression, it minimizes the Residual Sum of Squares ( or RSS or cost function ) to fit the training examples perfectly as possible. The cost function is also represented by J. Cost Function for Li
4 min read
Difference Between Ridge Regression and SVM Regressor in Scikit Learn
In this article, we will learn what is the difference between the two most common regression algorithms that is kernel Ridge Regression and SVR. And then we will move on to its code implementation using scikit learn in Python. What is Kernel ridge regression? Kernel ridge regression is a variant of ridge regression, which uses the kernel trick to l
4 min read
HuberRegressor vs Ridge on Dataset with Strong Outliers in Scikit Learn
Regression is a commonly used machine learning technique for predicting continuous outputs. In some datasets, outliers can have a significant impact on the results. To handle such datasets with outliers, two common algorithms are Huber Regressor and Ridge Regression. This article will explore the differences between the two algorithms in the contex
7 min read
Ordinary Least Squares and Ridge Regression Variance in Scikit Learn
In statistical modeling, Ordinary Least Squares (OLS) and Ridge Regression are two widely used techniques for linear regression analysis. OLS is a traditional method that finds the line of best fit through the data by minimizing the sum of the squared errors between the predicted and actual values. However, OLS can suffer from high variance and ove
7 min read
Ridge Regression in R Programming
Ridge regression is a classification algorithm that works in part as it doesn’t require unbiased estimators. Ridge regression minimizes the residual sum of squares of predictors in a given model. Ridge regression includes a shrinks the estimate of the coefficients towards zero. Ridge Regression in R Ridge regression is a regularized regression algo
5 min read
Multi-task lasso regression
MultiTaskLasso Regression is an enhanced version of Lasso regression. MultiTaskLasso is a model provided by sklearn that is used for multiple regression problems to work together by estimating their sparse coefficients. There is the same feature for all the regression problems called tasks. This model is trained with a mixed l1/l2 norm for regulari
2 min read
Article Tags :
Practice Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox