Beta Function
Last Updated :
16 Jun, 2020
The
Beta function is a unique function and is also called the first kind of Euler’s integrals. The beta function is defined in the domains of real numbers. The notation to represent it is “β”. The beta function is denoted by β(p, q), Where the parameters p and q should be real numbers.
It explains the association between the set of inputs and the outputs. Each input value the beta function is strongly associated with one output value. The beta function plays a major role in many mathematical operations.
Beta function is defined by-
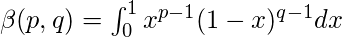
where p>0 and q>0
Some standard results:
-
Symmetry :
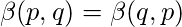
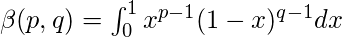 Put x=1-y
Put x=1-y
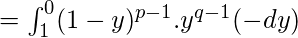
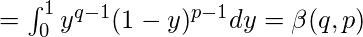
-
Beta function in terms of trigonometric functions :
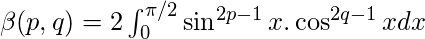
-
Beta function expressed as improper integral :
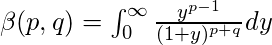
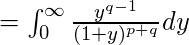
-
Relation between beta and gamma functions :
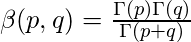
-
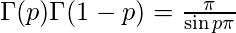 where 0<p<1
where 0<p<1
-
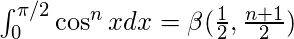
-
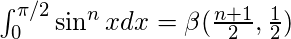
-
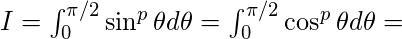
-
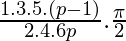 if p is an even positive integer
if p is an even positive integer
-
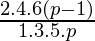 if p is an odd positive integer
if p is an odd positive integer
-
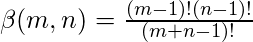 for m, n positive integers
for m, n positive integers
Example-1:
Evaluate
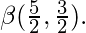 Explanation :
Explanation :
Using result (4) we get,
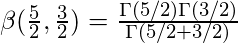
We know that
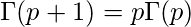
Thus we get
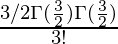
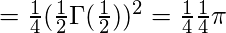
=0.1964
Example-2:
Evaluate
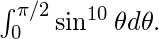 Explanation :
Explanation :
As p=10 is a positive integer, using result (8(i)) we get,
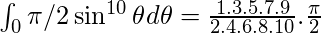
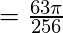 Example-3:
Example-3:
Evaluate
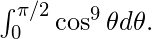 Explanation :
Explanation :
As p=9 is an odd positive integer, using result 8(ii) we get,
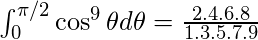
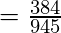
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...