Class 10 RD Sharma Solutions – Chapter 4 Triangles – Exercise 4.5 | Set 2

Question 13. The perimeters of two similar triangles are 25 cm and 15 cm, respect. If one side of the first triangle is 9 cm, what is the corresponding side of the other triangle?

Solution:

Given: perimeter of two similar triangles are 25 cm, 15 cm and one side 9 cm

To find : the other side.

Let the two triangles be ABC & PQR.

Let one of its side is (AB) = 9 cm and the other side of other triangle be PQ.

∆ABC ∼ ∆PQR.      [Since the ratio of corresponding sides of similar triangles is same as the ratio of their perimeters.]

AB/PQ = BC/QR = AC/PR = 25/15

9/PQ = 25/15

25 PQ = 15 × 9

PQ = (15×9)/25

PQ =(3× 9 )/5

PQ = 27/5

PQ =  5.4 cm

Hence, the corresponding side of other ∆ is 5.4 cm.

Question 14. In ΔABC and ΔDEF, it is being given that AB = 5 cm, BC = 4 cm, CA = 4.2 cm, DE = 10 cm, EF = 8 cm, and FD = 8.4 cm. If AL ⊥ BC, DM ⊥ EF, find AL: Dm.

Solution:

Given,

AB = 5 cm, BC = 4 cm, CA = 4.2 cm, DE = 10 cm, EF = 8 cm, and FD = 8.4 cm

AL ⊥ BC, DM ⊥ EF

To find: AL: DM

Now In ∆ABC and ∆DEF,

AB/DE=BC/EF=AC/DF=1/2   [both triangles are similar]

[In similar triangle the ratio of corresponding altitude is same as the ratio of the corresponding sides.]

   AL: DM = 1: 2

Question 15. D and E are the points on the sides AB and AC respectively, of a ΔABC such that AD = 8 cm, DB = 12 cm, AE = 6 cm, and CE = 9 cm. Prove that BC = 5/2 DE.

Solution:

AE/EC=6/9=2/3…….(1)

AD/DB=8/12=2/3……(2)

from (1) and (2) we know that 

AD/DB=AE/EC

 ED∥CB                                                

Now In△AED and △ACB,

 ED∥CB  

∠AED=∠ACB

∠ADE=∠ABC

△AED∼△ACB    [by AAA criteria]

 AE/AC=ED//CB

AE/EC+AE= ED/CB [AC=AE+EC]

6/6+9= ED/CB

6/15=2/5=ED/CB

CB=5/2ED  

 Hence proved

Question 16. D is the midpoint of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE: EX = 3 : 1

Solution:

Given: In ∆ABC, D is the midpoint of BC, E is the midpoint of AD. BE produced meets AC at X.

To prove :  BE: EX = 3 : 1

Now In Δ BCX  and  ΔDCY,

∠CBX  = ΔCBY   (corresponding angles)

∠CXB  = ΔCYD   (corresponding angles)

ΔBCX∼ΔDCY   (AA similarity)

BC/DC = BX/ DY = CX/CY    [ corresponding sides of two similar triangles are proportional]

BX/DY = BC/DC

BX/DY = 2DC/DC   [As D is the midpoint of BC]

BX/DY = 2/1…………(i)

Now In ΔAEX and ΔADY,

∠AEX  = ΔADY   (corresponding angles)

∠AXE = ΔAYD   (corresponding angles)

ΔAEX ∼ ΔADY   (AA similarity)

AE/AD = EX/DY = AX/AY  [ corresponding sides of two similar triangles are proportional]

EX/DY = AE/AD

EX/DY = AE/2AE                 [ D is the midpoint of BC]

EX/DY = ½…………..…(ii)

On Dividing eqn. (i) by eqn. (ii) we get,

BX/EX = 4/1

BX = 4EX

BE + EX = 4EX

BE = 4EX – EX

BE = 3EX

BE /EX = 3/1

BE : EX = 3:1

Hence proved

Question 17. ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.

Solution:

Given : ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q.

To prove : BP x DQ = AB x BC

Now In ∆ABP and ∆QDA,

∠B = ∠D [Opposite angles of parallelogram]

∠BAP = ∠AQD [Alternate interior angles]

 ∆ABP ~ ∆QDA [By AA similarity]

AB/QD = BP/DA   [the corresponding sides of similar triangles are proportional]

DA = BC  [opposite sides of a parallelogram are equal]

AB/QD = BP/BC

AB × BC = QD × BP

Hence proved

Question 18. In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respect. If Al and CM intersect at O, prove that:

(i) ΔOMA ∼ ΔOLC

(ii)OA/OC=OM/OL

Solution:

Given,

AL ⊥ BC and CM ⊥ AB

To prove:

(i)  ΔOMA ∼ ΔOLC

(ii)OA/OC=OM/OL

Now In Δ OMA and ΔOLC,

∠MOA = ∠LOC                [Vertically opposite angles]

∠AMO = ∠CLO                [Each 90°]

ΔOMA ~ ΔOLC       [By AA similarity]

OA/OC=OM/OL  [Corresponding parts of similar Δ are proportional]

Hence proved

Question 19. ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the midpoints of AB, AC, CD, and BD respect. Show that PQRS is a rhombus.

Solution:

Given, 

ABCD is a quadrilateral in which AD = BC and P, Q, R, S are the mid points of AB, AC, CD, BD, respectively.

To prove: PQRS is a rhombus

Now,

In ΔABC, P and Q are the mid points of the sides B and AC respectively

PQ ∥ BC and PQ = 1/2 BC.             [By the midpoint theorem]

In ΔADC, Q and R are the mid points of the sides AC and DC respectively

By the mid-point theorem, we get,

QR ∥ AD  QR = 1/2 AD    [By the mid-point theorem]

QR = 1/2 BC              [AD = BC]

Now In ΔBCD,

RS∥BC and RS = 1/2 AD  [By the mid-point theorem]

RS= 1/2 BC    [AD = BC]

From above eqns.

PQ = QR = RS

 PQRS is a rhombus.

Hence proved

Question 20. In an isosceles ΔABC, the base AB is produced both ways to P and Q such that AP x BQ = AC2. Prove that Δ APC ∼ Δ BCQ

Solution:

Given : ΔABC is isosceles ∆ and AP x BQ = AC²

To prove : ΔAPC∼ΔBCQ.

we know that, 

ΔABC is an isosceles triangle AC = BC.

AP x BQ = AC²  (given)

AP x BQ = AC x AC

AP x BQ = AC x BC

AP/BC = ABQ……….(1).

so, ∠CAB = ∠CBA    [as  AC = BC]

180° – ∠CAP = 180° – ∠CBQ [angles opposite to equal sides are EQUAL]

∠CAP = ∠CBQ ………..(2)

In ∆APC and ΔBCQ

AP/BC = AC/BQ [From equation 1]

∠CAP = ∠CBQ [From equation 2]

ΔAPC∼ΔBCQ  [By SAS similarity criterion]

Hence proved

Question 21. A girl of height 90 cm is walking away from the base of a lamp post at a speed of 1.2 m/sec. If the lamp is 3.6m above the ground, find the length of her shadow after 4 seconds.

Solution:

AD=1.2 m/sec ×4 sec =4.8 m =480 cm

Suppose the length of the shadow of the girl be x cm when she at position D. Therefore,

BD = x cm

In ∆BDE and ∆BAC,

∠BDE=∠BAC  [each90°]

∠DBE=∠ABC   [Common angle ]

 ∆BDE∼∆BAC   [ by AA similarity]

BE/BC=DE/AC=BD/AB  [Corresponding sides are proportional]

90/360=x/480+x

1/4= x/480+x

4x=480+x

4x−x=480

3x=480

x=480/3=160

Hence, the length of her shadow after 4 seconds is 160 cm.

Question 22. A vertical stick of length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28m long. Find the height of the tower.

Solution:

Let AB be stick and DE be tower.

A 6 m long stick casts a shadow of 4 m 

So,  AB = 6 m and BC = 4 m

Let DE casts shadow at the same time, So EF = 28 m

Let height of tower DE = x

Now in ∆ABC and ∆DEF,

∠B = ∠E (each 90°)

∠C = ∠F (shadows at the same time)

∆ABC ~ ∆DEF     [AA criterion]

AB/DE=BC/EF      [ Corresponding sides are proportional ]

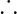6/x=4/28

x=42 m

Hence height of tower is 42 m

Question 23. In the fig. given, ΔABC is a right-angled triangle at C and DE ⊥ AB. Prove that ΔABC ∼ ΔADE. hence find the lengths of AE and DE.

Solution:

Given : ΔACB is right-angled triangle at C = 90°.

According to the figure : BC = 12 cm , AD=3 cm, DC = 2 cm.

AC = AD + DC = 3 +2= 5 cm

Now In ∆ACB,

AB² = AC² + BC² [by Pythagoras theorem]

AB² = 5² + 12²

AB² = 25 + 144 = 169

AB= √169 = 13  

AB = 13 cm

Now In  ΔABC & ΔADE,

∠BAC = ∠DAE     [common]

∠ACB = ∠AED      [each 90°]

ΔABC∼ΔADE     [by AA similarity criterion]

AB/AD = BC/DE = AC/AE    [ corresponding sides of two similar triangles are proportional]

13/3 = 12/ DE = 5/AE

13/3 = 12/DE

13 DE = 12×3  

DE = 36/13

13/3 = 5/AE

13 AE = 5×3

AE = 15/13

Hence, the length of DE= 36/13 & AE = 15/13

Question 24. In the figure, PA, QB and RC are each perpendicular to AC. Prove that 1/X+1/Z=1/Y

Given:

PA, QB and RC are each perpendicular to AC

To prove : 1/X+1/Z=1/Y

Now In ΔPAC and ΔQBC,

∠PCA = ∠QCB  [common angle]

∠PAC = ∠QBC [Corresponding angles]

ΔPAC ~ ΔQBC [by AA criteria]

PA/QB = AC/BC  [ Corresponding parts of similar triangles are proportional]

x/y = AB/BC  

y/x = BC/AC

Now In ΔRCA and ΔQBA,

∠RAC = ∠QAB [common angle]

∠RCA = ∠QBA [Corresponding angle]

ΔRCA ~ΔQBA  [by AA criteria]

RC/QB = AC/AB [ Corresponding parts of similar triangles are proportional]

z/y= AC/AB

y/z= AB/AC

y/z + y/z = BC + AC/ AC = 1  [by adding both eq we get]

y/z + y/z = 1

1/x + 1/z = 1/y [multiplying both sides by y]

Hence proved

Question 25. In fig. given, we have AB ∥ CD ∥ EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm, and DE = y cm. Calculate the values of x and y.

Solution:

Given : AB || CD || EF , AB = 6 cm, CD = x cm, BD = 4 cm, and DE = y cm and EF = 10 cm.

Now In ∆ECD and ∆EAB,

∠CED = ∠AEB    [common]

∠ECD = ∠EAB   [corresponding angles]

∆ECD ~ ∆EAB ……….(1) [By AA similarity]

∴ EC/EA = CD/AB   [Corresponding parts of similar triangles are proportional]

EC / EA = x/6 ……………(2)

In ∆ACD and ∆AEF

∠CAD = ∠EAF [common]

∠ACD = ∠AEF [corresponding angles]

∆ACD ~ ∆AEF [By AA similarity]

∴ AC/AE = CD/EF     [Corresponding parts of similar triangles are proportional]

AC /AE = x/10 ……………..(3)

EC/EA+ AC /AE =  x/6 + x/10  [by Adding eq 2 & 3]

(EC + AC) /AE =( 5x + 3x)/30

AE / AE = 8x /30

1 = 8x/30

x = 30/8  

x = 3.75 cm

∆ECD ~ ∆EAB    [From eq  (i)]

DC/AB = ED /EB   [Corresponding parts of similar triangle are proportional]

3.75/6 = y/y+4

6y = 3.75(y+4)

6y = 3.75y + 15

6y – 3.75y = 15

2.25y = 15

y = 15/2.25

y = 6.67 cm

Hence, x = 3.75 cm and y = 6.67 cm.