Class 11 NCERT Solutions- Chapter 9 Sequences And Series – Exercise 9.4

Last Updated : 21 Feb, 2021

Find the sum to n terms of each of the series in Exercises 1 to 7.

Question 1. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …

Solution:

Given: Series = 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …

To find nth term, we have

n^th term, a_n = n ( n + 1)

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}k(k+1)\\ =\sum^n_{k=1}k^2+\sum^n_{k=1}k\\ =\frac{n(n+1)(2n+1)}{6}+\frac{n(n+1)}{2}\\ =\frac{n(n+1)}{2}\left(\frac{2n+1}{3}+1\right)\\ =\frac{n(n+1)}{2}\left(\frac{2n+4}{3}\right)\\ =\frac{n(n+1)(n+2)}{3}$

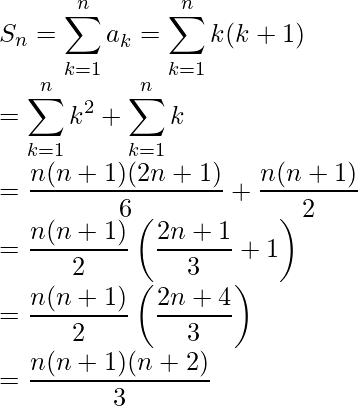
Question 2. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …

Solution:

Given: Series = 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …

To find nth term, we have

n^th term, a_n = n(n + 1)(n + 2)

= (n² + n) (n + 2)

= n³ + 3n² + 2n

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}k^3+3\sum^n_{k=1}k^2+2\sum^n_{k=1}k\\ =\left[\frac{n(n+1)}{2}\right]^2+\frac{3n(n+1)(2n+1)}{6}+\frac{2n(n+1)}{2}\\ =\left[\frac{n(n+1)}{2}\right]^2+\frac{n(n+1)(2n+1)}{2}+n(n+1)\\ =\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+2n+1+2\right]\\ =\frac{n(n+1)}{2}\left[\frac{n^2+n+4n+6}{2}\right]\\ =\frac{n(n+1)}{4}(n^2+5n+6)\\ =\frac{n(n+1)}{4}(n^2+2n+3n+6)\\ =\frac{n(n+1)[n(n+2)+3(n+2)]}{4}\\ =\frac{n(n+1)(n+2)(n+3)}{4}$

Question 3. 3 × 1² + 5 × 2² + 7 × 3² + …

Solution:

Given: Series = 3 × 1² + 5 × 2² + 7 × 3² + …

To find nth term, we have

n^thterm, a_n = (2n + 1) n² = 2n³ + n²

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}(2k^3+k^2)=2\sum^n_{k=1}k^3+\sum^n_{k=1}k^2\\ =2\left[\frac{n(n+1)}{2}\right]^2+\frac{n(n+1)(2n+1)}{6}\\ =\frac{n^2(n+1)}{2}+\frac{n(n+1)(2n+1)}{6}\\ =\frac{n(n+1)}{2}\left[n(n+1)+\frac{2n+1}{3}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+3n+2n+1}{3}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+5n+1}{3}\right]\\ =\frac{n(n+1)(3n^2+5n+1)}{6}$

Question 4. Find the sum to n terms of the series

$\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+....$

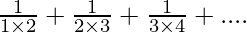
Solution:

Given: Series = 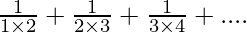$\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+....$

To find nth term, we have

n^thterm a_n = $\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$ (By partial fractions)

$a_1=\frac{1}{1}-\frac{1}{2}\\ a_2=\frac{1}{2}-\frac{1}{3}\\ a_3=\frac{1}{3}-\frac{1}{4}...\\ a_n=\frac{1}{n}-\frac{1}{n+1}$

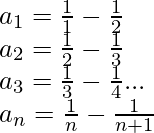
So, on adding the above terms columns wise, we obtain

$a_1+a_2+...+a_n=\left[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+....\frac{1}{n}\right]-\left[\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\frac{1}{n+1}\right]\\ \therefore S_n=1-\frac{1}{n+1}=\frac{n+1-1}{n+1}=\frac{n}{n+1}$

Question 5. Find the sum to n terms of the series 5² + 6² + 7² + … + 20²

Solution:

Given: Series = 5² + 6² + 7² + … + 20²

To find nth term, we have

n^th term, a_n = (n + 4)² = n² + 8n + 16

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}(k^2+8k+16)\\ =\sum^n_{k=1}k^2+8\sum^n_{k=1}k+\sum^n_{k=1}16\\ =\frac{n(n+1)(2n+1)}{6}+\frac{8n(n+1)}{2}+16n$

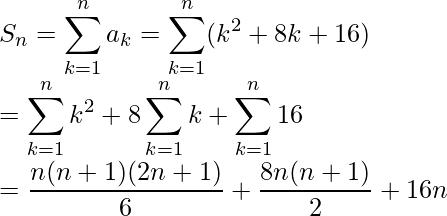
16^th term is (16 + 4) = 20²

$S_{16}=\frac{16(16+1)(2\times16+1)}{6}+\frac{8\times16\times(16+1)}{2}+16\times16\\ =\frac{(16)(17)(33)}{6}+\frac{(8)\times(16)\times(16+1)}{2}+16\times16\\$

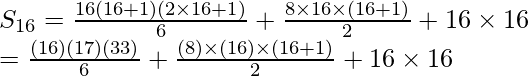
= 1496 + 1088 + 256

= 2840

So, 5² + 6² + 7² + …..+ 20² = 2840

Question 6. Find the sum to n terms of the series 3 × 8 + 6 × 11 + 9 × 14 +…

Solution:

Given: Series = 3 × 8 + 6 × 11 + 9 × 14 + …

To find nth term, we have

a_n = (n^th term of 3, 6, 9 …) × (n^th term of 8, 11, 14, …)

= (3n) (3n + 5)

= 9n² + 15n

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}(9k^2+15k)\\ =9\sum^n_{k=1}k^2+15\sum^n_{k=1}k\\ =9\times\frac{n(n+1)(2n+1)}{6}+15\times\frac{15n(n+1)}{2}\\ =\frac{3n(n+1)}{2}(2n+1+5)\\ =\frac{3n(n+1)}{2}(2n+6)$

= 3n(n + 1)(n +3)

Question 7. Find the sum to n terms of the series 1² + (1² + 2²) + (1² + 2² + 3²) + …

Solution:

Given: Series = 1² + (1² + 2²) + (1² + 2² + 3²⁾ + …

To find nth term, we have

a_n = (1² + 2² + 3² +…….+ n²)

$=\frac{n(n+1)(2n+1)}{6}\\ =\frac{n(2n^2+3n+1)}{6}\\ =\frac{2n^3+3n^2+n}{6}\\ =\frac{1}{3}n^3+\frac{1}{2}n^2+\frac{1}{6}n$

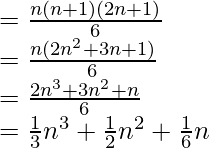
So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}\left(\frac{1}{3}k^3+\frac{1}{2}k^2+\frac{1}{6}k\right)\\ =\frac{1}{3}\sum^n_{k=1}k^3+\frac{1}{2}\sum^n_{k=1}k^2+\frac{1}{6}\sum^n_{k=1}k\\ =\frac{1}{3}\frac{n^2(n+1)^2}{(2)^2}+\frac{1}{2}\times\frac{n(n+1)(2n+1)}{6}+\frac{1}{6}\times\frac{n(n+1)}{2}\\ =\frac{n(n+1)}{6}\left[\frac{n(n+1)}{2}+\frac{(2n+1)}{2}+\frac{1}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{n^2+n+2n+2}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{n(n+1)+2(n+1)}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{(n+1)(n+2)}{2}\right]\\ =\frac{n(n+1)^2(n+2)}{12}$

Question 8. Find the sum to n terms of the series whose n^th term is given by n (n + 1) (n + 4).

Solution:

Given: a_n = n (n + 1) (n + 4) = n(n² + 5n + 4) = n³ + 5n² + 4n

Now, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}k^3+5\sum^n_{k=1}k^2+4\sum^n_{k=1}\\ =\frac{n^2(n+1)^2}{4}+\frac{5n(n+1)(2n+1)}{6}+\frac{4n(n+1)}{2}\\ =\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+\frac{5(2n+1)}{3}+4\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+3n+20n+10+24}{6}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+23n+34}{6}\right]\\ =\frac{n(n+1)(3n^2+23n+34)}{12}$

Question 9. Find the sum to n terms of the series whose nth terms is given by n² + 2ⁿ

Solution:

Given: n^th term of the series as:

a_n = n² + 2ⁿ

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}k^2+2^k=\sum^n_{k=1}k^2+\sum^n_{k=1}2^k\ \ \ \ \ \ (1)$

$\displaystyle\sum^n_{k=1}2^k=2^1+2^2+2^3+......$

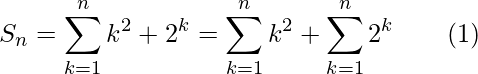
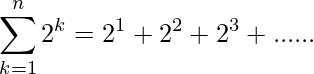
Now, the above series 2, 2², 2³ ….. is G.P.

and the first term and common ration is equal to 2.

$\therefore\displaystyle\sum^n_{k=1}2^k=\frac{(2)[(2)^n-1]}{2-1}=2(2^n-1)\ \ \ \ \ (2)$

From eq(1) and (2), we get

$S_n=\displaystyle\sum^n_{k=1}k^2+2(2^n-1)=\frac{n(n+1)(2n+1)}{6}+2(2n-1)$

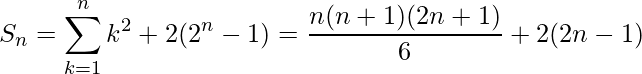
Question 10. Find the sum to n terms of the series whose n^th terms is given by (2n – 1)²

Solution:

Given: n^thterm of the series as:

a_n = (2n – 1)² = 4n² – 4n + 1

So, the sum of n terms of the series:

$S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}(4k^2-4k+1)\\ =4\sum^n_{k=1}-4\sum^n_{k+1}k+\sum^n_{k=1}1\\ =\frac{4n(n+1)(2n+1)}{6}-\frac{4n(n+1)}{2}+n\\ =\frac{2n(n+1)(2n+1)}{3}-2n(n+1)+n\\ =n\left[\frac{2(2n^2+3n+1)}{3}-2(n+1)+1\right]\\ =n\left[\frac{4n^2+6n+2-6n-6+3}{3}\right]\\ =n\left[\frac{4n^2-1}{3}\right]\\ =\frac{n(2n+1)(2n-1)}{3}$

Suggest improvement

Class 11 NCERT Solutions- Chapter 9 Sequences And Series - Exercise 9.3 | Set 2

Class 11 NCERT Solutions- Chapter 9 Sequences And Series - Miscellaneous Exercise On Chapter 9 | Set 1

Share your thoughts in the comments

Chapter 1: Sets

Chapter 2: Relations and Functions

Chapter 3: Trigonometric Functions

Chapter 4: Principle of Mathematical Induction

Chapter 5: Complex Numbers and Quadratic Equations

Chapter 6: Linear Inequalities

Chapter 7: Permutations and Combinations

Chapter 8: Binomial Theorem

Chapter 9: Sequences and Series

Chapter 10: Straight Lines

Chapter 11: Conic Sections

Chapter 12: Introduction to Three-dimensional Geometry

Chapter 13: Limits and Derivatives

Chapter 14: Mathematical Reasoning

Chapter 15: Statistics

Chapter 16: Probability

Class 11 NCERT Solutions- Chapter 9 Sequences And Series – Exercise 9.4

Find the sum to n terms of each of the series in Exercises 1 to 7.

Question 1. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …

Question 2. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …

Question 3. 3 × 12 + 5 × 22 + 7 × 32 + …

Question 4. Find the sum to n terms of the series

Question 5. Find the sum to n terms of the series 52 + 62 + 72 + … + 202

Question 6. Find the sum to n terms of the series 3 × 8 + 6 × 11 + 9 × 14 +…

Question 7. Find the sum to n terms of the series 12 + (12 + 22) + (12 + 22 + 32) + …

Question 8. Find the sum to n terms of the series whose nth term is given by n (n + 1) (n + 4).

Question 9. Find the sum to n terms of the series whose nth terms is given by n2 + 2n

Question 10. Find the sum to n terms of the series whose nth terms is given by (2n – 1)2

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?

Question 3. 3 × 1² + 5 × 2² + 7 × 3² + …

Question 5. Find the sum to n terms of the series 5² + 6² + 7² + … + 20²

Question 7. Find the sum to n terms of the series 1² + (1² + 2²) + (1² + 2² + 3²) + …

Question 8. Find the sum to n terms of the series whose n^th term is given by n (n + 1) (n + 4).

Question 9. Find the sum to n terms of the series whose nth terms is given by n² + 2ⁿ

Question 10. Find the sum to n terms of the series whose n^th terms is given by (2n – 1)²