Class 11 RD Sharma Solutions – Chapter 24 The Circle – Exercise 24.3

Question 1. Find the equation of the circle, the end points of whose diameter are (2, -3) and (-2, 4). Find its radius and centre.

Solution:

Given that the end points of the diameter are (2, -3) and (-2, 4).

So, the equation of the circle is

(x – 2)(x + 2) + (y + 3)(y – 4) = 0

x² – 4 + y² – y – 12 = 0

x² + y² – y – 16 = 0        ……(1)

From eq(1), we get

2g = 0, 2f = -1           

g = 0, f = -1/2 

The center of the circle is(0, 1/2) 

And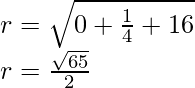 

Question 2. Find the equation of the circle, the endpoints of whose diameter are centers of the circles x² + y² + 6x – 14y – 1 = 0 and x² + y² – 4x + 10y – 2 = 0.

Solution:

Given equations are

x² + y² + 6x – 14y – 1 = 0

It can also written as

(x + 3)² + (y – 7)² = 59  ……(i)

x² + y² – 4x + 10y – 2y – 1 = 0

It can also written as

(x – 2)² + (y + 5)² = 31  ……(ii)

So, from eq(i) and (ii)

the centres of the circles are (-3, 7) and (2,-5)

Now the equation of the circle is  

(x – x1)(x – x2) + (y – y1)(y – y2) = 0

(x + 3)(x – 2) + (y – 7)(y + 5) = 0

x² + 3x – 2x – 6 + y² – 7y + 5y – 35 = 0

x² + y² + x – 2y – 41 = 0

Question 3. The sides of a square are x = 6, x = 9, y = 3, and y = 6. Find the equation of a circle drawn on the diagonal of the square as its diameter.  

Solution:

Let us considered AB, BC, CD, and DA are the sides of the square ABCD be resented by the given equations  

y = 3, x = 6, y = 6 and x = 9 

So, the coordinates are

A(6, 3), B(9, 3), C(9, 6) and D(6, 6)

So, the equation of the circle with diagonal AC

(x – 6)(x – 9) + (4 – 3)(4 – 6) = 0

x² – 6x – 9x + 54 + y² – 3y – 6y + 18 = 0

x² + y² – 15x – 9y + 72 = 0

And the equation of the circle with diagonal BD as diameter is  

(x – 9)(x – 6) + (y – 3)(y – 6) = 0

x² – 9x – 6x + 54 + y² – 3y – 6y + 18 = 0

x² + y² – 15x – 9y + 72 = 0

x² + y² – 15 – 9y + 72 = 0

Question 4. Find the equation of a circle circumscribing the rectangle whose sides are x – 2y = 4, 3x + y = 22, x – 3y = 14 and 3x + y = 62.

Solution:

The given equations of the sides of the rectangle are

x – 3y = 4       ———– (i)

3x + y = 22    ———–(ii)

x – 3y = 14     ———–(iii)

3x + y = 62    ———-(iv)

Let us assume A, B, C, and D are the points intersection of the lines (i), (ii), (iii), and (iv)

So, A(7, 1), B(8, -2), C(20, 2) and D(19, 5)

AC will be the diameter of the circle

Hence, the equation of circle is

(x – 7)(x – 20) + (y – 1)(y – 2) = 0

x² + y² – 27x – 3y + 142 = 0

Question 5. Find the equation of the circle passing through the origin and the points where the line 3x + 4y = 12 meets the axes of coordinates.

Solution:

Given equation of line is 3x + 4y = 12

So, it will meet the axis at A(0, 3) and B(4, 0)

Since the circle passes through origin A and B

So, AB is a diameter

Hence, the equation of circle is  

(x – 0)(x – 4) + (y – 3)(y – 0) = 0

x² + y² – 4x – 3y = 0

Question 6. Find the equation of the circle which passes through the origin and cuts off intercepts a and b respectively y from x and y-axes.

Solution:

It is given that the circle is passes through origin and cut intercept a and b on  

x-axis and y-axis

So, the coordinates of circle A(0, b) and B(a, 0)

Here, AB is the diameter of the circle

Hence, the equation of the circle is  

(x – a)(x – 0) + (y – 0)(y – b) = 0

x² + y² ± ax ± by = 0

Question 7. Find the equation of the circle whose diameter is the line segment joining (-4, 3) and (12, -1). Find also the intercept made by it on y-axis.  

Solution:

Given that the line segment A(-4, 3) and B(12, -1) is joining a diameter

So, the equation of circle in diameter form is,

(x + 4)(x – 12) + (y – 3)(y + 1) = 0

x² – 8x – 48 + y² – 2y – 3 = 0

x² – 8x – 2y + y² – 51 = 0 ……(1)

To find y-intercept, put x = 0 in eq(1), we get

y² – 2y – 51 = 0

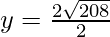
So, y intercepts are 1 ± 4√13

Question 8. The abscissae of the two points A and B are the roots of the equation x² + 2ax – b² = 0 and their coordinates are the roots of the equation x² + 2px – q² = 0. Find the equation of the circle with AB as diameter. Also, find its radius.  

Solution:

The given equations are

x² + 2ax – b² = 0 ……..(i)

x² + 2px – q² = 0 ………(ii)

Now root of eq(i)

and roots of eq(ii)

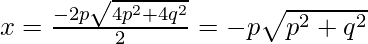
So, the coordinates of A = ()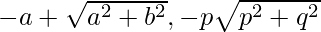

and B = ()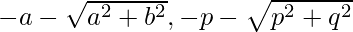

So, the equation of circle is  

x² + y² + 2ax + 2py – (a² + b² + p² + q²) + a² + p² = 0

x² + y² + 2ax + 2py – (b² + q²) = 0

Hence, the radius is

Question 9. ABCD is a square whose side is a, taking AB and AD as axes, prove that the equation of the circle circumscribing the square is x² + y² – a(x + y) = 0.

Solution:

Given that, ABCD is a square whose side is a.

Also, given that AD and AD are axes, so point of intersection is (0, 0)

Also, the other point on the diagonal of the square will have coordinates (a, a).

It is given that equation of the circle circumscribe the square.

So, (0, 0) and (a, a) will be the end points of the diameter of the circle.

So, the equation of the circle is 

(x – 0)(x – a) + (y – 0)(y – a) = 0

x² – ax + y² – ay = 0

x² + y² – a(x + y) = 0

Question 10. The line 2x – y + 6 = 0 meets the circle x² + y² – 2y – 9 = 0 at A and B. Find the equation of the circle on AB as diameter.

Solution:

The given equations of line and circle are

2x – y + 6 = 0        ……(i)

x² + y² – 2y – 9 = 0   …….(ii)

The point of intersection of eq (i) and (ii) is

x² + (2x + 6)² – 2(2x + 6) – 9 = 0

x² + 4x² + 24x + 36 – 4x – 12 – 9 = 0

5x² + 20x + 15 = 0

(x + 3)(x + 1) = 0                  

⇒ x = (-3, -1)

and  y = (0, 4)

So, point A(-3, 0) and B(-1, 4)

Here, AB is a diameter, so the equation of circle is

(x + 3)(x + 1) + (y – 0)(y – 4) = 0

x² + y² + 4x – 4y + 3 = 0

Question 11. Find the equation of the circle which circumscribes the triangle formed by the lines x = 0, y = 0, and lx + my = 1.

Solution:

The given equations of lines are

x = 0   …….(i)

y = 0     …….(ii)

lx + my = 1   …….(iii)

The line eq(iii) cuts the axis at

A(0, 1/m) and B(1/l, 0)

Now, AB will be the diameter of circle,

So, the equation of circle will be,

(x – 1/l)(x – 0) + (y – 0)(y – 1/m) = 0

x² + y² – x/l – y/m = 0

Question 12. Find the equations of the circle which passes through the origin and cut of equal chords of √2 units from the lines y = x and y = -x.

Solution:

Let the angles between y = x and y = -x is π/2

So, the angle between OB and OA = π/2

Hence, AB, BC, CD and AD are diameter of circles.

so, ∠BOQ = π/4

sin∠BOQ = BQ/OB

sin π/4 = BQ/√2

1/√2 = BQ/√2

BQ = 1

So, the radius of circle(OQ) = 1 

And the coordinates of B is (1, 1)

Similarly, coordinates of A(-1, 1), C(1, -1), D(-1, -1)

Now the equation of circle with diameter AB is  

(x + 1)(x – 1) + (y – 1)(y – 1) = 0

x² – 2x + 1 + y² – 1 = 0

x² + y² – 2x = 0

The equation of circle with diameter BC is

(x – 1)(x – 1) + (y – 1)(y + 1) = 0

x² – 2x + 1 + y² – 1 = 0

x² + y² – 2x = 0

The equation of circle with diameter CD is  

(x + 1)(x – 1) + (y + 1)(y + 1) = 0

x² – 1 + y² + 2y + 1 = 0

x² + y² + 2y = 0

And the equation of circle with diameter AD is

(x + 1)(x + 1) + (y – 1)(y + 1) = 0

x² + 2x + 1 + y² – 1 = 0

x² + y² + 2x = 0