Class 9 NCERT Solutions- Chapter 10 Circles – Exercise 10.6

Question 1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.  

Solution:

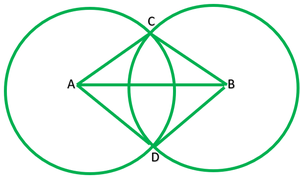
Given: Two circles with Centre A and B circle intersects at C and D.

To prove: ∠ACB=∠ADB

Construction: Join AD,BC and BD

Proof: In ∆ACB and ∆ADB

AC=AD            ——–[radii of the same circle]

BC=BD           ———[radii of the same circle]

AB=AB            ——–[common]

∴∆ACB≅∆ADB     ——— [by  S.S.S]

∠ACB=∠ADB          ——–[c.p.c.t.]

Question 2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.

Solution:

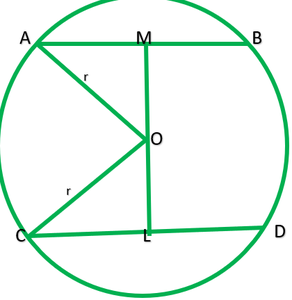
Let O be the centre of circle and be r cm

Given: AB=5cm, CD =11cm

Construction: Draw OM perpendicular AB  and  OL perpendicular CD.

Because OM perpendicular AB  and  OL perpendicular CD and AB||CD.

∴Points O,L, and  M are collinear, than ∠M=6cm  

Let OL=x  

Then OM=6=x

Join AO and CO

OA=OC =r

OL=1/2CD=1/2*11=5.5cm  —–[perpendicular from bisects the chord]

AM=1/2AB=1/2*5=2.3cm   —–[perpendicular from bisects the chord]

Now, In right ∆DLC

r²=(OL)²+(CL)²

r²=x²+(5.5)²

r²=x²+30.25       ———–1

Now in right ∆OMA

r²=(OM)²+(MA)²

r²=(6-x)²+(2.5)²

r²=36+x²=12x+6.25

r²=x²-12x+42.25             ———–2

Now equating equation 1 and 2

X²+30.25=x²-12x+30.25

12x=42.25-30.25

X=12/12=1

Putting value of x in equation 1

r²=x²+30.25

r²=(1)²+30.25

r²=31.25

r=√31.25=5.6  (approx.)

Radius of circle is 5.6cm.

Question 3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the center, what is the distance of the other chord from the centre?

Solution:

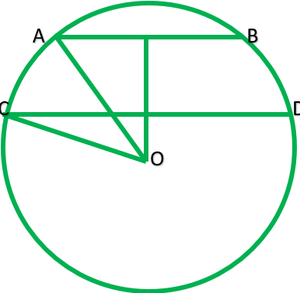
Let AB and CD are|| chord of circle with centre O which AB=6cm and CD=8cm and radius of circle =r cm.

Construction: Draw OP perpendicular AB  and OM perpendicular CD.

Because AB||CD and OP perpendicular AB and OM perpendicular CD therefore. Point O, M and P are collinear.

Clearly, OP=4cm ———-[According to question]

OM=to find?

P is midpoint of AB.

∴AP=1/2 AB=1/2*6=3cm  

M is midpoint of AB.

CM=1/2 CD=1/2*8cm=4cm

Join AO and CO

Now in Right ∆OPA,

r²=AP²+PO²

r²=3²+4²

r²=9+16=25

Now in ∆OMC

r²=CM²+MO²

25=4²+MO²

25-16=MO²

9=MO²

√9=MO  

3=MO

∴Therefore distance of the other chord from the centre is 3cm  

Question 4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.  

Solution:

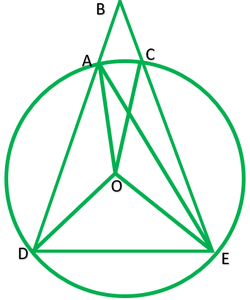
Give: Vertex B of ∆ABC lie outside the circle,chord AD=CE

To prove: ∠ABC=1/2(∠DOE-∠AOC)

Construction: Join AE

Solution: Chord DE subtends ∠DOE at the center and ∠DAE at point A on the circle.

∴∠DAE=1/2∠DOE       ———-1

chords AC subtends ∠AOC at the centre and ∠AEC at point  

∴∠AEC=1/2∠AOC          ———2

In ∆ ABE,∠DAE is exterior angle  

∠DAE=∠ABC +∠AEC  

1/2∠DOE=∠ABC+1/2∠AOC

½(∠DOE-∠AOC)= ∠ABC

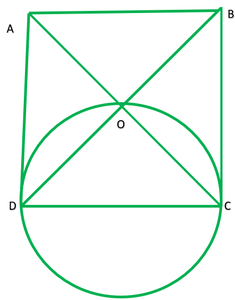
Question 5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.

Solution:

Given: A rhombus ABCD in which O is intersecting point of diagonals AC and BD.

A circle is drawn taking CD as diameter.

To prove: circle points through O or Lies on the circles.

Proof: In rhombus ABCD,

∠DOA=90°       ——–[diagonals of rhombus intersect at 90°] 1

In circle:

∠COD=90° ——–[angle made in segment  O is right angle] 2

From 1 and 2

O lies on the circle.

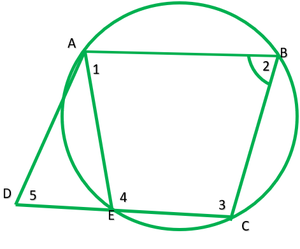
Question 6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.  

Solution:

ABCD is a ||gm. The  circle through A,B and C intersect at E.

To prove: AE=AD

Proof: Here ABCE is a cyclic quadrilateral

∠2+∠4=180°      —–[sum of opposite is of a cyclic quadrilateral is 180°]

∠4=180°-∠1     ——-1

Now ∠4+∠6=180°-∠6         ———2

From 1 and 2

180°-∠2=∠180°-∠6

∠2=∠6          ———–3

Also ∠2=∠5       ———[opposite angles of ||gm are equal]        —–4

From 3 and 4

∠5=∠6

Now, In ∆ADE,

∠5=∠6

∴AE=AD        ——[sides apposite to equal angles in  a∆ are equal]

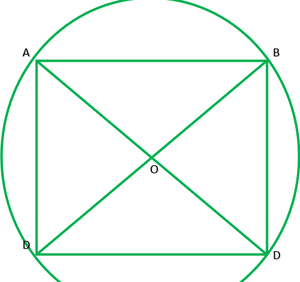
Question 7. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.

 Solution:

Given: Two chords AC and BD bisects each other i.e OA=OC,OB=OD

To prove: In ∆AOB and COB

AO=CO        ——-[given]

∠AOB=∠COD    ——[vertically opposite angle]

OB=OD         ——–[give]

∴∆AOB≅∆COB   ——[s.s.s]

AB=CD   ——[C.P.C.T.]         1

similarly ∆AOD≅∆COB   (S.A.S)

AD=CD           (C.P.C.T.)   2

From 1 and 2     ABCD is a ||gm

Since, ABCD  is cyclic quadrilateral

∴∠A+∠C=180°  

∠B+∠B=180°

2∠B=180°

∠B=180°/2

∠B=90°

∴ ∠A  and ∠B lies in a semicircle

→ AC and BD are diameter of circle.

ii) Since ABCD is a ||gm and ∠A=90°

∴ ABCD is a rectangle.

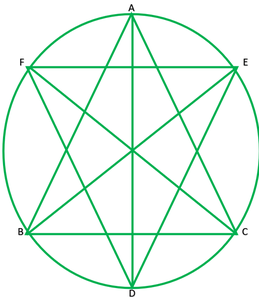
Question 8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – 1 2 A, 90° – 1 2 B and 90° – 1 2 C.

Solution:

Given:∆ABC and it circum-circle AD,BE and CF are bisectors of ∠A,∠B and ∠C  

Respectively.

To proof:∠ D=90°-1/2∠A ,    ∠E=90°-1/2∠B    ,  ∠F=90°-1/2∠C

Construction: Join AE and AF.

Solution: ∠ADE=∠ABE       ———-1  [angle in the same segment are equal]

              ∠ADF=∠ACF      ———–2 [angle in the same segment are equal]

Adding 1 and 2

∠ADE+∠ABF=∠ABE+∠ACF

∠D=1/2∠B+1/2∠C  ——[BC and CF are bisector of ∠B & ∠c]

∠D=1/2(∠B+∠C)

∠D=1/2(180°-∠A)

∠D=1/2(180°-∠A)

∠D=90°-1/2∠AC

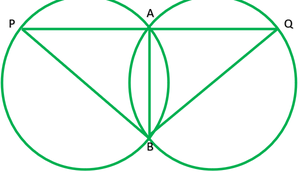
Question 9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.  

Solution:

Given: two congruent circles which intersect at A and B.  

PAB is a line segment

To prove: BA=BQ

Construction: join AB

Proof: AB is a common chord of both the congruent circle.

Segment of both circles will be equal

∠P=∠Q

Now, in ∆ BPQ,

∠P=∠Q

BP=BQ       ——[sides opposite to equal angles are equal]

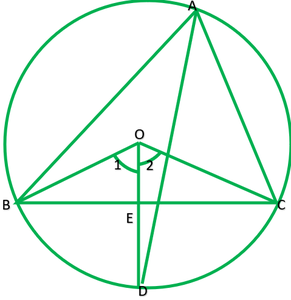
Question 10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.

 Solution:

Given: A ∆ABC, in which AD is angle bisector of ∠A and OD is ⊥ bisector of BC.

To prove: D lies on circumcircle.

Construction: Join OB and OC

Proof: Since BC subtends ∠BAC at A on the remaining of the circle.

∠BOC=2∠BAC               ——-1

Now, In ∆BOE and ∆ COE

BO=OE      ——–(radii of the same circle)

BE=CE        —–(give)

∴∆BOE≅COE       ——-(S.S.S)

∠1=∠2                     ——-(c.p.c.t)

Now,

∠1+∠2=∠BOC

2∠1=∠BOC

2∠1=2∠BAC         ———- (from 1)

∠1=∠BAC

∠BOE=∠BAF

∠BOD=∠BAC

∠BOD=2∠BAD        [AD is bisector of ∠BAC]

This is possible only if BD is chord of the circle.

D lies on the circle.