Collisions in Two Dimensions

A Collision occurs when a powerful force strikes on two or more bodies in a relatively short period of time. Collision is a one-time occurrence. As a result of the collision, the involved particles’ energy and momentum change. The collision may occur as a result of actual physical contact between the participating bodies, such as a collision between two billiard balls or a ball and bat. There may be collisions where there is no direct physical touch, such as an alpha particle colliding with a nucleus.

Any collision is led by three different definable stages, namely before, during, and after the impact. Because the particles are independent before the collision, the interaction forces between them are zero. Furthermore, following the impact, the force returns to zero. Because the particles come into touch with each other during the collision, the force of interaction becomes extremely strong. The dominant forces direct the movement of the bodies. Because the amount of the interacting force is unknown in most practical circumstances, Newton’s second law of motion cannot be used in such cases. The initial and final velocities can be computed using the law of conservation of momentum.

For instance, consider two bodies with masses m₁ and m₂, moving with velocities u₁ and u₂. They undergo a collision due to the application of an external force F_ext for a small interval of time, and then the final velocities become v₁ and v₂.

Two Dimensional Elastic Collisions

The following cases may arise in case of elastic collision between two bodies : 

(1) Two-dimensional Elastic Collision in Laboratory Reference Frame

Let us consider a system of two particles without the existence of any external forces. The first particle of mass m₁ moving with an initial velocity of 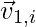 and the second particle of mass m₂ which is initially at rest position. The interacting particles undergo a collision where the first particle moves with velocity  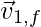 and the second particle with velocity . The reference frame with one particle at rest can be termed as the target, the laboratory reference frame. 

The angles θ_1,f and θ_2,f made by the particles along with the positive forward direction of the first particle are called the laboratory scattering angles.

The problem statement is to determine the magnitudes and directions of each of the final velocity vectors, 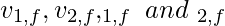. The total kinetic energy and momentum are conserved in the whole system. 

The components of the total momentum are obtained by, 

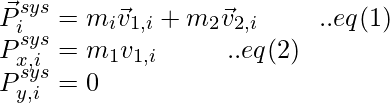
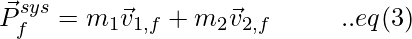
The components of momentum in the final state are obtained by, 

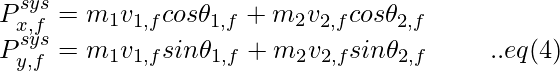
Since, the total momentum is conserved, we get,

Further from above equations, we obtain, 

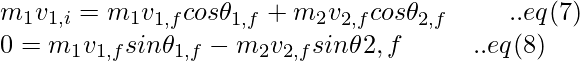
Since, the kinetic energy is preserved during an elastic collision,

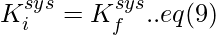
Computing eq(7), 

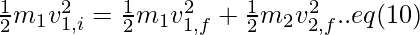
Rewriting eq(5) and eq (6) as,

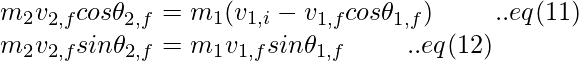
Squaring and adding each of the expressions in eq (9) and eq(10), 

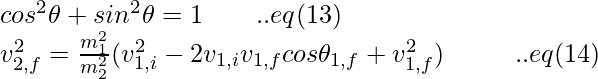
Substituting the eq (11) into eq (8), we obtain, 

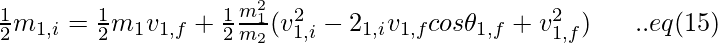
Simplifying eq (12), we get,

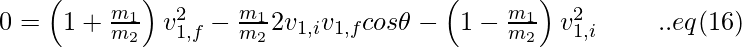
Let ∝ =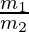  

Rewriting eq (13) ,

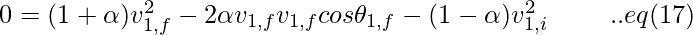
Finding solution of quadratic equation, we can obtain the following results, 

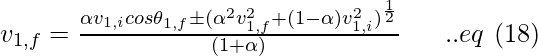
Computing for eq (9),

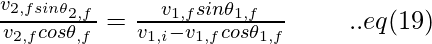
Simplifying eq (16), we get,

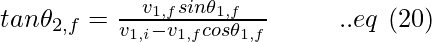
We can conclude that the relationship between the scattering angles is independent of the masses of the colliding particles. 

Therefore, 

the scattering angle for the second particle can be computed by,

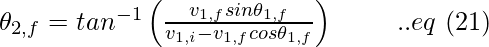
Using eq (10), in order to compute the final velocity of the first particle, 

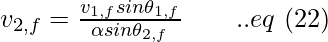
(2) Elastic collision with infinite masses in two dimensions 

Let us assume a body to be of mass m₁colliding with an infinite mass at rest. Let us assume its velocity be u_n along the normal before collision and in the tangential direction to be u_t      

Since the momentum is conserved in the tangential direction,

m₁u_t = mv_1,t

v_1,t = u_t

Since the momentum is conserved in the normal direction,

m₁u_n = m₁v_1,n + m2v_2n

In case of elastic collision between bodies, the velocity of approach equals the velocity of separation, therefore, 

v_2,n – v_1,n = u_n

Simplifying, we obtain, 

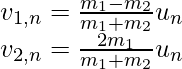
On approximating, we use, m2 >> m1

v_1,n = -u_1,n

v_2,n = 0

(3) Elastic collision of equal masses in two dimensions 

Let us assume a body to be of mass m. The second body holds the same mass m and is initially at rest.  The two interacting particles undergo collision.  Let us assume the velocity to be u_n along the normal before collision and u_t along the tangent.  

Since the momentum is conserved in the tangential direction,

mu_t = mv_1,t

v_1,t = u_t

Since the momentum is conserved in the normal direction,

mu_n = mv_1,n + mv_2,n

In case of elastic collision between bodies, the velocity of approach equals the velocity of separation, therefore, 

v_2,n – v_1,n = u_n

The equation can be further solved to obtain, 

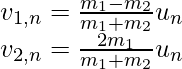
Since, the masses are equal , we get, m₂ = m₁

v_1,n = 0

that is, 

v_2,n = u_n

(4) Inelastic Collision in Two Dimension

For a completely inelastic collision, let us assume a system consisting of two particles m₁ with velocity v₁ and m₂  with velocity v₂ at an angle of θ₁ with respect to each other. After the inelastic collision, both the masses form a single mass M and move with a final velocity v_f.

The law of conservation of energy is not applicable in an inelastic collision. The equations of momentum can be generated for masses in both the x and y directions, by shifting the orientation of the object with mass m₁ in the x-axis direction. 

Now, we obtain, 

x component: m₁v₁ + Mv_fcosθ₂

y component: m₂v₂sinθ₁ Mv_fsinθ₂

The final result leaves us with two-equation and two variables, v_f, and θ₂. Thus, any completely inelastic collision in two dimensions is easily solvable in comparison to the completely elastic collision.

Deflection of a moving particle by a particle at rest

Let us assume a system of two masses, m₁  moving with a velocity u₁ and the second body of mass m₂ to be at rest. After the collision, the first mass object starts moving with a velocity of v₁ and gets deflected by the angle θ₁ in the incident direction. Similarly, the second mass object starts moving with a velocity of v₂ and gets deflected by the angle θ₂ in the incident direction.

Now, we have, 

According to the law of conservation of linear momentum ,

For components along the x-axis, we have, 

m₁u₁ = m₁v₁cosθ₁ +m₂v₂cosθ₂   .. eq(1)

For components along y-axis,  we have, 

0=m₁v₁sinθ₁ -m₂v₂sinθ₂   ..eq(2)

Since, the system reduces to the availability of three equations and four unknown variables, solving the system with only these values becomes impossible. 

Sample Problems

Problem 1: A mass of 10 kg is traveling with a velocity of 30 m/s in the positive y-axis. The mass undergoes a collision with another object of mass 40 g moving along the negative y-axis at a speed of 50 m/s. Calculate the final velocity. 

Solution:

According to the law of conservation of momentum, therefore, 

Momentum before impact = Momentum After Impact

Equating the values, we get, 

10 × 30 + (.04) × (-50) = 10.04 v

Since, the 40g particle is moving in negative direction, we have, 

v = 29.68 m/s

Problem 2: There is an isolated system containing three masses, m₁ = m₂ = 2 m and m₃ = 3 m. All the masses travel in direction, but with the same initial velocity equivalent to v₀. The bodies collide and undergo an elastic collision. Compute the maximal possible final speed of each of the three bodies.

Solution:

Total initial kinetic energy in the system = 

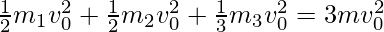
The maximum speed is attained when the speeds of other particles is reduced to zero. 

Therefore,

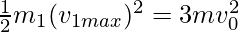
Substituting the values of the masses, 

We get, 

v_1max = 2.45v₀

v_2max = 1.73v₀

v_3max = 1.41v₀

Problem 3: A sphere moving with a velocity vector strikes a vertical wall. The wall is parallel to the velocity vector. The coefficient of restitution between the sphere and wall is e. What is the velocity vector of the sphere on hitting the ball?

Solution:

Computing the value, 

v_y = 2 m/s

v_x = -e × 2 = -1 m/s

 

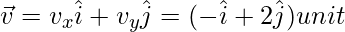
Problem 4: Consider a body of mass m kg moving with a speed u. The ball hits the floor elastically with an angle of incidence, in such a way, that the velocity before and after the collision remains the same. Also, the angle of rebound equals the angle of incidence. Let us assume the velocity towards the floor to be negative. What will be the change in momentum taken parallel to the surface?

Solution:

Since, we know, that the force acting on the body of mass ‘m’ is the normal reaction force of the surface. The change in momentum taken parallel to the surface will be equivalent to 0, since no parallel force acts on the ball.

Problem 5: Explain the aftermath repercussions when two unequal masses collide. 

Solution:

When two bodies of unequal mass collide, the force acting on both objects is not equal and opposite in nature. Both the interacting particles experience unequal accelerations during the collision because of the contact forces.