Dial’s Algorithm (Optimized Dijkstra for small range weights)

Last Updated : 23 Jun, 2023

Dijkstra’s shortest path algorithm runs in O(Elog V) time when implemented with adjacency list representation (See C implementation and STL based C++ implementations for details).

Input : Source = 0, Maximum Weight W = 14
Output :
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14

Consider the below Graph:

The shortest path from source 0

We have learned about how to find the shortest path from a given source vertex to all other vertex using Dijkstra’s shortest path algorithm with the Time Complexity of O(E log V) in this article.

Can we optimize Dijkstra’s shortest path algorithm to work better than O(E log V) if the maximum weight is small (or the range of edge weights is small)?

For example, in the above diagram, the maximum weight is 14. Many times the range of weights on edges is in a small range (i.e. all edge weights can be mapped to 0, 1, 2.. w where w is a small number). In that case, Dijkstra’s algorithm can be modified by using different data structures, and buckets, which is called dial implementation of Dijkstra’s algorithm. time complexity is O(E + WV) where W is the maximum weight on any edge of the graph, so we can see that, if W is small then this implementation runs much faster than the traditional algorithm.

The following are important observations.

The maximum distance between any two nodes can be at max w(V – 1) (w is maximum edge weight and we can have at max V-1 edges between two vertices).
In the Dijkstra algorithm, distances are finalized in non-decreasing, i.e., the distance of the closer (to given source) vertices is finalized before the distant vertices.

Algorithm

Below is the complete algorithm:

Maintains some buckets, numbered 0, 1, 2,…,wV.
Bucket k contains all temporarily labeled nodes with a distance equal to k.
Nodes in each bucket are represented by a list of vertices.
Buckets 0, 1, 2,..wV are checked sequentially until the first non-empty bucket is found. Each node contained in the first non-empty bucket has the minimum distance label by definition.
One by one, these nodes with minimum distance labels are permanently labeled and deleted from the bucket during the scanning process.
Thus operations involving vertex include:
- Checking if a bucket is empty
- Adding a vertex to a bucket
- Deleting a vertex from a bucket.
The position of a temporarily labeled vertex in the buckets is updated accordingly when the distance label of a vertex changes.
The process is repeated until all vertices are permanently labeled (or the distances of all vertices are finalized).

Implementation

Since the maximum distance can be w(V – 1), we create wV buckets (more for simplicity of code) for implementation of the algorithm which can be large if w is big.

C++

// C++ Program for Dijkstra's dial implementation
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f
 
// This class represents a directed graph using
// adjacency list representation
class Graph
{
    int V; // No. of vertices
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    list< pair<int, int> > *adj;
 
public:
    Graph(int V); // Constructor
 
    // function to add an edge to graph
    void addEdge(int u, int v, int w);
 
    // prints shortest path from s
    void shortestPath(int s, int W);
};
 
// Allocates memory for adjacency list
Graph::Graph(int V)
{
    this->V = V;
    adj = new list< pair<int, int> >[V];
}
 
// adds edge between u and v of weight w
void Graph::addEdge(int u, int v, int w)
{
    adj[u].push_back(make_pair(v, w));
    adj[v].push_back(make_pair(u, w));
}
 
// Prints shortest paths from src to all other vertices.
// W is the maximum weight of an edge
void Graph::shortestPath(int src, int W)
{
    /* With each distance, iterator to that vertex in
    its bucket is stored so that vertex can be deleted
    in O(1) at time of updation. So
    dist[i].first = distance of ith vertex from src vertex
    dist[i].second = iterator to vertex i in bucket number */
    vector<pair<int, list<int>::iterator> > dist(V);
 
    // Initialize all distances as infinite (INF)
    for (int i = 0; i < V; i++)
        dist[i].first = INF;
 
    // Create buckets B[].
    // B[i] keep vertex of distance label i
    list<int> B[W * V + 1];
 
    B[0].push_back(src);
    dist[src].first = 0;
 
    //
    int idx = 0;
    while (1)
    {
        // Go sequentially through buckets till one non-empty
        // bucket is found
        while (B[idx].size() == 0 && idx < W*V)
            idx++;
 
        // If all buckets are empty, we are done.
        if (idx == W * V)
            break;
 
        // Take top vertex from bucket and pop it
        int u = B[idx].front();
        B[idx].pop_front();
 
        // Process all adjacents of extracted vertex 'u' and
        // update their distanced if required.
        for (auto i = adj[u].begin(); i != adj[u].end(); ++i)
        {
            int v = (*i).first;
            int weight = (*i).second;
 
            int du = dist[u].first;
            int dv = dist[v].first;
 
            // If there is shorted path to v through u.
            if (dv > du + weight)
            {
                // If dv is not INF then it must be in B[dv]
                // bucket, so erase its entry using iterator
                // in O(1)
                if (dv != INF)
                    B[dv].erase(dist[v].second);
 
                // updating the distance
                dist[v].first = du + weight;
                dv = dist[v].first;
 
                // pushing vertex v into updated distance's bucket
                B[dv].push_front(v);
 
                // storing updated iterator in dist[v].second
                dist[v].second = B[dv].begin();
            }
        }
    }
 
    // Print shortest distances stored in dist[]
    printf("Vertex Distance from Source\n");
    for (int i = 0; i < V; ++i)
        printf("%d     %d\n", i, dist[i].first);
}
 
// Driver program to test methods of graph class
int main()
{
    // create the graph given in above figure
    int V = 9;
    Graph g(V);
 
    // making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);
 
    // maximum weighted edge - 14
    g.shortestPath(0, 14);
 
    return 0;
}
 
// This code is contributed by Aditya Kumar (adityakumar129)

Python3

from typing import List, Tuple
INF = 0x3f3f3f3f
 
# This class represents a directed graph using adjacency list representation
class Graph:
    def __init__(self, V: int):
        # No. of vertices
        self.V = V
         
        # In a weighted graph, we need to store vertex and weight pair for every edge
        self.adj = [[] for _ in range(V)]
 
    # function to add an edge to graph
    def addEdge(self, u: int, v: int, w: int):
        self.adj[u].append((v, w))
        self.adj[v].append((u, w))
 
    # Prints shortest paths from src to all other vertices.
    # W is the maximum weight of an edge
    def shortestPath(self, src: int, W: int):
        # With each distance, iterator to that vertex in its bucket is stored so that vertex can be deleted
        # in O(1) at time of updation. So dist[i][0] = distance of ith vertex from src vertex
        # dist[i][1] = iterator to vertex i in bucket number
        dist = [[INF, None] for _ in range(self.V)]
 
        # Initialize distance of source vertex
        dist[src][0] = 0
 
        # Create buckets B[].
        # B[i] keep vertex of distance label i
        B = [[] for _ in range(W * self.V + 1)]
        B[0].append(src)
 
        idx = 0
        while True:
            # Go sequentially through buckets till one non-empty bucket is found
            while len(B[idx]) == 0 and idx < W * self.V:
                idx += 1
 
            # If all buckets are empty, we are done.
            if idx == W * self.V:
                break
 
            # Take top vertex from bucket and pop it
            u = B[idx][0]
            B[idx].pop(0)
 
            # Process all adjacents of extracted vertex 
            # 'u' and update their distances if required.
            for v, weight in self.adj[u]:
                du = dist[u][0]
                dv = dist[v][0]
 
                # If there is shorted path to v through u.
                if dv > du + weight:
                    # If dv is not INF then it must be in 
                    # B[dv] bucket, so erase its entry using iterator
                    # in O(1)
                    if dv != INF:
                        B[dv].remove(v)
 
                    # updating the distance
                    dist[v][0] = du + weight
                    dv = dist[v][0]
 
                    # pushing vertex v into updated distance's bucket
                    B[dv].append(v)
 
                    # storing updated iterator in dist[v][1]
                    dist[v][1] = len(B[dv]) - 1
 
        # Print shortest distances stored in dist[]
        print("Vertex Distance from Source")
        for i in range(self.V):
            print(f"{i}     {dist[i][0]}")
 
# Driver program to test methods of graph class
def main():
    # create the graph given in above figure
    V = 9
    W = 14
    g = Graph(V)
 
    g.addEdge(0, 1, 4)
    g.addEdge(0, 7, 8)
    g.addEdge(1, 2, 8)
    g.addEdge(1, 7, 11)
    g.addEdge(2, 3, 7)
    g.addEdge(2, 8, 2)
    g.addEdge(2, 5, 4)
    g.addEdge(3, 4, 9)
    g.addEdge(3, 5, 14)
    g.addEdge(4, 5, 10)
    g.addEdge(5, 6, 2)
    g.addEdge(6, 7, 1)
    g.addEdge(6, 8, 6)
    g.addEdge(7, 8, 7)
 
    g.shortestPath(0, W)
 
if __name__ == "__main__":
    main()
     
# This code is contributed by sanjanasikarwar24

C#

// C# Program for Dijkstra's dial implementation
using System;
using System.Collections.Generic;
 
// This class represents a directed graph using
// adjacency list representation
public class Graph 
{
  static readonly int INF = Int32.MaxValue;
  private int V; // No. of vertices
  // In a weighted graph, we need to store vertex
  // and weight pair for every edge
  private List<Tuple<int, int> >[] adj;
 
  public Graph(int v) // Constructor
  {
    this.V = v;
    this.adj = new List<Tuple<int, int> >[ v ];
    for (int i = 0; i < v; i++)
      this.adj[i] = new List<Tuple<int, int> >();
  }
 
  // function to Add an edge to graph
  // Adds edge between u and v of weight w
  public void AddEdge(int u, int v, int w)
  {
    adj[u].Add(Tuple.Create(v, w));
    adj[v].Add(Tuple.Create(u, w));
  }
 
  // Prints shortest paths from src to all other vertices.
  // W is the maximum weight of an edge
  public void shortestPath(int src, int W)
  {
    /* With each distance, iterator to that vertex in
        its bucket is stored so that vertex can be deleted
        in O(1) at time of updation. So
        dist[i].first = distance of ith vertex from src
        vertex dits[i].second = iterator to vertex i in
        bucket number */
    int[] dist = new int[V];
 
    // Initialize all distances as infinite (INF)
    for (int i = 0; i < V; i++)
      dist[i] = INF;
 
    // Create buckets B[].
    // B[i] keep vertex of distance label i
    List<int>[] B = new List<int>[ W * V + 1 ];
    for (int i = 0; i < W * V + 1; i++)
      B[i] = new List<int>();
 
    B[0].Add(src);
    dist[src] = 0;
 
    int idx = 0;
    while (true) {
      // Go sequentially through buckets till one
      // non-empty bucket is found
      while (B[idx].Count == 0 && idx < W * V)
        idx++;
 
      // If all buckets are empty, we are done.
      if (idx == W * V)
        break;
 
      // Take top vertex from bucket and pop it
      int u = B[idx][0];
      B[idx].Remove(u);
 
      // Process all adjacents of extracted vertex 'u'
      // and update their distances if required.
      foreach(Tuple<int, int> i in adj[u])
      {
        int v = i.Item1;
        int weight = i.Item2;
 
        int du = dist[u];
        int dv = dist[v];
 
        // If there is shorted path to v through u.
        if (dv > du + weight) {
          // updating the distance
          dist[v] = du + weight;
          dv = dist[v];
 
          // pushing vertex v into updated
          // distance's bucket
          B[dv].Insert(0, v);
        }
      }
    }
 
    // Print shortest distances stored in dist[]
    Console.WriteLine("Vertex Distance from Source");
    for (int i = 0; i < V; ++i)
      Console.WriteLine("{0}     {1}", i, dist[i]);
  }
}
 
class GFG {
  // Driver program to test methods of graph class
  static void Main(string[] args)
  {
    // create the graph given in above figure
    int V = 9;
    Graph g = new Graph(V);
 
    // making above shown graph
    g.AddEdge(0, 1, 4);
    g.AddEdge(0, 7, 8);
    g.AddEdge(1, 2, 8);
    g.AddEdge(1, 7, 11);
    g.AddEdge(2, 3, 7);
    g.AddEdge(2, 8, 2);
    g.AddEdge(2, 5, 4);
    g.AddEdge(3, 4, 9);
    g.AddEdge(3, 5, 14);
    g.AddEdge(4, 5, 10);
    g.AddEdge(5, 6, 2);
    g.AddEdge(6, 7, 1);
    g.AddEdge(6, 8, 6);
    g.AddEdge(7, 8, 7);
 
    // maximum weighted edge - 14
    g.shortestPath(0, 14);
  }
}
 
// This code is contributed by cavi4762

Javascript

// JS Program for Dijkstra's dial implementation
const INF = 0x3f3f3f3f;
 
// This class represents a directed graph using
// adjacency list representation
class Graph {
  constructor(V)
  {
    this.V = V;// No. of vertices
     
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    this.adj = Array.from({ length: V }, () => []);
  }
 
// adds edge between u and v of weight w
  addEdge(u, v, w) {
    this.adj[u].push([v, w]);
    this.adj[v].push([u, w]);
  }
   
// Prints shortest paths from src to all other vertices.
// W is the maximum weight of an edge
  shortestPath(src, W)
  {
   
       /* With each distance, iterator to that vertex in
    its bucket is stored so that vertex can be deleted
    in O(1) at time of updation. So
    dist[i].first = distance of ith vertex from src vertex
    dits[i].second = iterator to vertex i in bucket number */
    const dist = Array.from({ length: this.V }, () => [INF, null]);
    dist[src][0] = 0;
 // Create buckets B[].
    // B[i] keep vertex of distance label i
    const B = Array.from({ length: W * this.V + 1 }, () => []);
    B[0].push(src);
 
    let idx = 0;
    while (true)
    {
     
        // Go sequentially through buckets till one non-empty
        // bucket is found
      while (B[idx].length === 0 && idx < W * this.V) {
        idx += 1;
      }
      if (idx === W * this.V) {
        break;
      }
      const u = B[idx].shift();
       
    // Process all adjacents of extracted vertex 'u' and
        // update their distanced if required.
      for (const [v, weight] of this.adj[u]) {
        const du = dist[u][0];
        let dv = dist[v][0];
         
       // If there is shorted path to v through u.
        if (dv > du + weight)
        {
         
               // If dv is not INF then it must be in B[dv]
                // bucket, so erase its entry using iterator
                // in O(1)
          if (dv !== INF) {
            B[dv].splice(dist[v][1], 1);
          }
           
           // updating the distance
          dist[v][0] = du + weight;
          dv = dist[v][0];
           
                // pushing vertex v into updated distance's bucket
          B[dv].push(v);
           
          // storing updated iterator in dist[v].second
          dist[v][1] = B[dv].length - 1;
        }
      }
    }
     
 // Print shortest distances stored in dist[]
    console.log("Vertex Distance from Source");
    for (let i = 0; i < this.V; i++) {
      console.log(`${i}     ${dist[i][0]}`);
    }
  }
}
 
// Driver code
  const V = 9;
  const W = 14;
  const g = new Graph(V);
 
  g.addEdge(0, 1, 4);
  g.addEdge(0, 7, 8);
  g.addEdge(1, 2, 8);
  g.addEdge(1, 7, 11);
  g.addEdge(2, 3, 7);
  g.addEdge(2, 8, 2);
  g.addEdge(2, 5, 4);
  g.addEdge(3, 4, 9);
  g.addEdge(3, 5, 14);
  g.addEdge(4, 5, 10);
  g.addEdge(5, 6, 2);
  g.addEdge(6, 7, 1);
  g.addEdge(6, 8, 6);
  g.addEdge(7, 8, 7);
 
  g.shortestPath(0, W);
 
// This code is contributed by lokeshpotta20.

Java

import java.util.*;
 
public class Graph {
    static final int INF = Integer.MAX_VALUE;
    private int V; // No. of vertices
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    private ArrayList<ArrayList<Tuple> > adj;
 
    public Graph(int v) // Constructor
    {
        this.V = v;
        this.adj = new ArrayList<ArrayList<Tuple> >();
        for (int i = 0; i < v; i++)
            this.adj.add(new ArrayList<Tuple>());
    }
 
    // function to Add an edge to graph
    // Adds edge between u and v of weight w
    public void AddEdge(int u, int v, int w)
    {
        adj.get(u).add(new Tuple(v, w));
        adj.get(v).add(new Tuple(u, w));
    }
 
    // Prints shortest paths from src to all other vertices.
    // W is the maximum weight of an edge
    public void shortestPath(int src, int W)
    {
        /* With each distance, iterator to that vertex in
            its bucket is stored so that vertex can be
           deleted in O(1) at time of updation. So
            dist[i].first = distance of ith vertex from src
            vertex dits[i].second = iterator to vertex i in
            bucket number */
        int[] dist = new int[V];
 
        // Initialize all distances as infinite (INF)
        Arrays.fill(dist, INF);
 
        // Create buckets B[].
        // B[i] keep vertex of distance label i
        ArrayList<Integer>[] B = new ArrayList[W * V + 1];
        for (int i = 0; i < W * V + 1; i++)
            B[i] = new ArrayList<Integer>();
 
        B[0].add(src);
        dist[src] = 0;
 
        int idx = 0;
        while (true) {
            // Go sequentially through buckets till one
            // non-empty bucket is found
            while (B[idx].size() == 0 && idx < W * V)
                idx++;
 
            // If all buckets are empty, we are done.
            if (idx == W * V)
                break;
 
            // Take top vertex from bucket and pop it
            int u = B[idx].get(0);
            B[idx].remove(0);
 
            // Process all adjacents of extracted vertex 'u'
            // and update their distances if required.
            for (Tuple i : adj.get(u)) {
                int v = i.v;
                int weight = i.w;
 
                int du = dist[u];
                int dv = dist[v];
 
                // If there is shorted path to v through u.
                if (dv > du + weight) {
                    // updating the distance
                    dist[v] = du + weight;
                    dv = dist[v];
 
                    // pushing vertex v into updated
                    // distance's bucket
                    B[dv].add(0, v);
                }
            }
        }
 
        // Print shortest distances stored in dist[]
        System.out.println("Vertex Distance from Source");
        for (int i = 0; i < V; ++i)
            System.out.println(i + "\t\t" + dist[i]);
    }
 
    static class Tuple {
        int v, w;
        Tuple(int v, int w)
        {
            this.v = v;
            this.w = w;
        }
    }
    public static void main(String[] args)
    {
        // create the graph given in above figure
        int V = 9;
        Graph g = new Graph(V);
 
        // making above shown graph
        g.AddEdge(0, 1, 4);
        g.AddEdge(0, 7, 8);
        g.AddEdge(1, 2, 8);
        g.AddEdge(1, 7, 11);
        g.AddEdge(2, 3, 7);
        g.AddEdge(2, 8, 2);
        g.AddEdge(2, 5, 4);
        g.AddEdge(3, 4, 9);
        g.AddEdge(3, 5, 14);
        g.AddEdge(4, 5, 10);
        g.AddEdge(5, 6, 2);
        g.AddEdge(6, 7, 1);
        g.AddEdge(6, 8, 6);
        g.AddEdge(7, 8, 7);
 
        // maximum weighted edge - 14
        g.shortestPath(0, 14);
    }
}

Output

Vertex Distance from Source
0     0
1     4
2     12
3     19
4     21
5     11
6     9
7     8
8     14

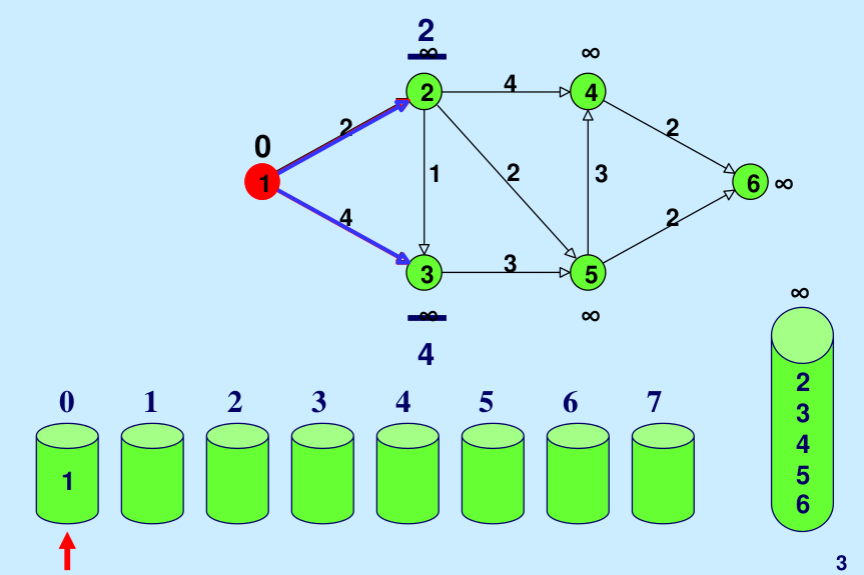
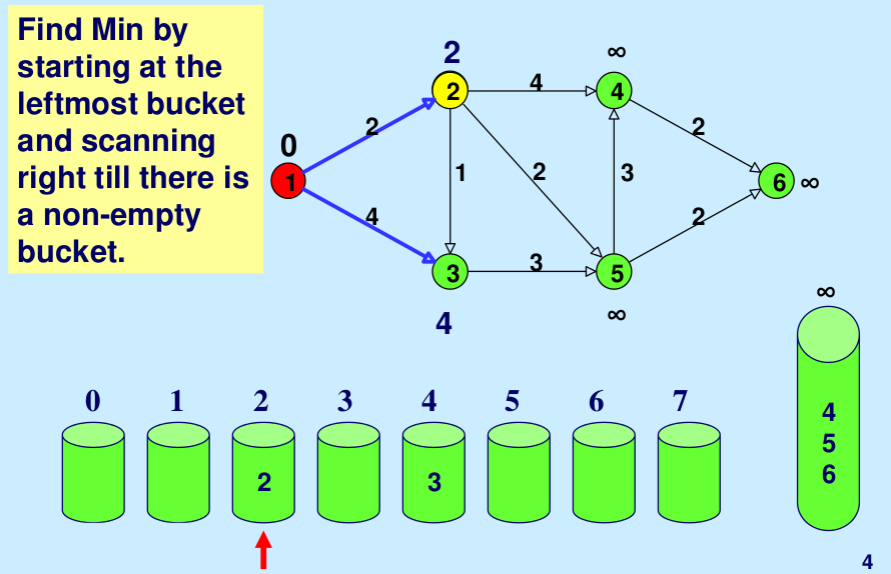
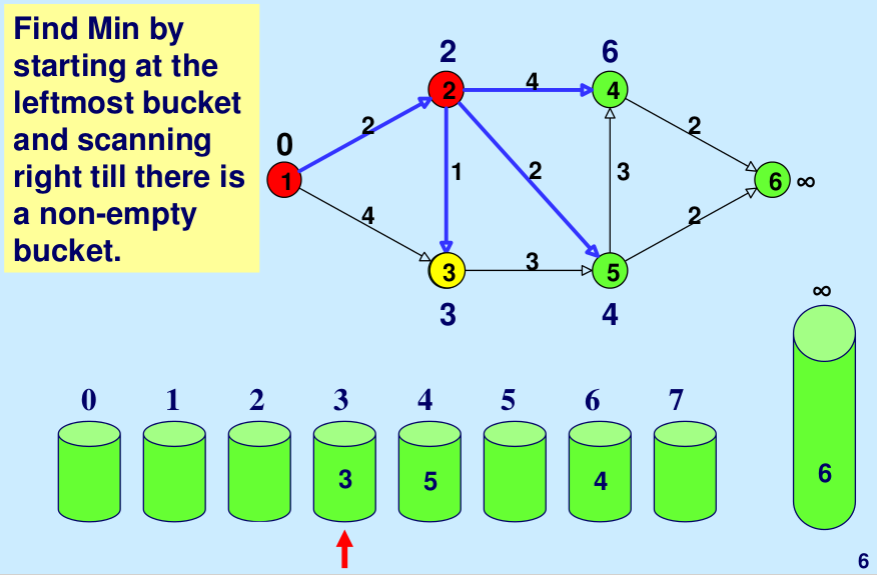
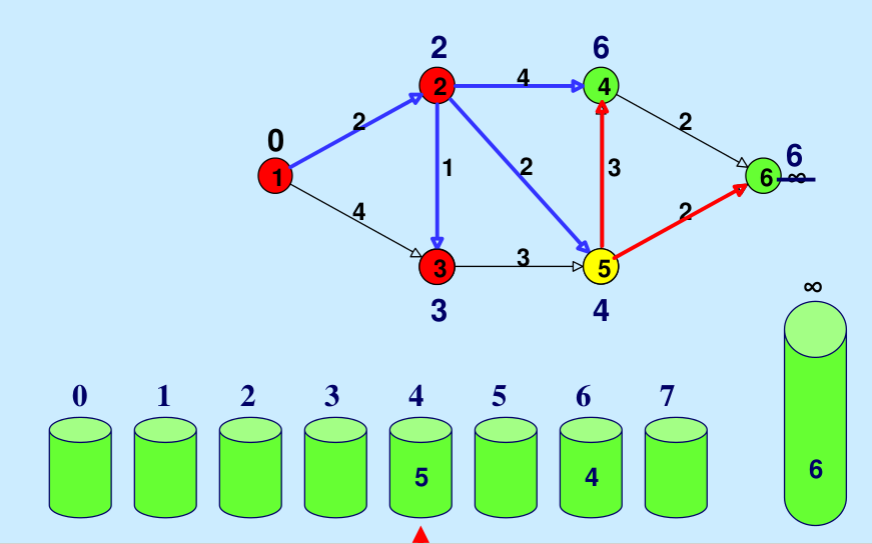
Illustration: Below is the step-by-step illustration taken from here.

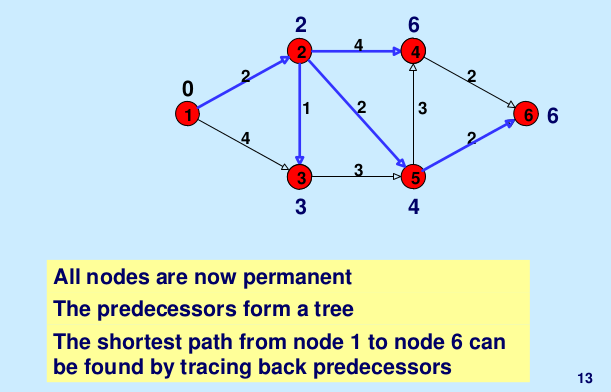
Time Complexity: The time complexity of the above implementation is O(V*W). Here V is the number of vertices in the graph and W is the maximum weight of the edge.

Space Complexity: The space complexity of the above implementation is O(V*W). In the above implementation, we have used a 2D vector to store the distances of each vertex from the source vertex.

Dial’s algorithm is an optimized version of Dijkstra’s algorithm for finding the shortest paths in a graph with non-negative edge weights. It is particularly useful when the range of the edge weights is small, meaning that the weights only take on a small number of distinct values.

Here are the steps of Dial’s algorithm:

Initialize a set of buckets, where each bucket i contains all nodes with a current shortest path estimate of i.
Start with the source node s and set its shortest path estimate to 0.
For each node v adjacent to s, add it to the bucket corresponding to its distance from s.
While there are non-empty buckets:
a. Find the non-empty bucket with the smallest index i.
b. Remove the node u with the smallest shortest path estimate from the bucket.
c. For each node v adjacent to u:
If the shortest path estimate for v is greater than the new estimate via u, update v’s estimate and move it to the corresponding bucket.
Return the shortest path estimates for all nodes.
The idea behind Dial’s algorithm is to avoid scanning all nodes in each iteration of Dijkstra’s algorithm. Instead, we group the nodes into buckets based on their shortest path estimate, and only process the nodes with the smallest estimate in each iteration. This reduces the number of nodes that need to be processed and speeds up the algorithm, especially when the range of the edge weights is small.

Advantages:

Dial’s algorithm can be much faster than Dijkstra’s algorithm for graphs with small range weights.
It has a time complexity of O(n + m), where n is the number of nodes and m is the number of edges.
It is easy to implement and modify from Dijkstra’s algorithm.

Disadvantages:

Dial’s algorithm is only applicable when the range of the edge weights is small. For graphs with large range weights, Dijkstra’s algorithm may be faster.
The space complexity of Dial’s algorithm is O(nW), where W is the range of the edge weights. This can be a significant drawback for large values of W.

Suggest improvement

Boruvka's algorithm | Greedy Algo-9

Minimum cost to connect all cities

Share your thoughts in the comments

Standard Greedy algorithms

Greedy algorithm on Array

Greedy algorithm on Operating System

Greedy algorithm on Graph

Approximate Greedy algorithm for NP complete problems

Greedy algorithm for special cases of DP

Some easy problems on Greedy algorithm

Some medium level problems on Greedy algorithm

Some hard problems on Greedy algorithm