Derivative of a Function is the rate of change in the given function with respect to an independent variable. The derivative of a given function in Calculus is found using the First Principle of differentiation. The process of finding the derivative of a function is also called the Differentiation of function.
Derivative of a Function gives the slope of the particular function at the point of differentiation and is used to get the extreme value of the function. It is also defined as the rate of change of the function with respect to any point lying in the domain of the function. A function f(x) is differentiable at a point x = a if it is continuous at that point.
In this article, we will learn about the Derivative of a function, the First Principle of Differentiation, the Differentiation of Trig Function, the Differentiation of Exponential Function, and others in detail.
What is Derivative of A Function
Derivative of a Function is the slope of the function at any particular point in the domain of the function. We know that every function represents a curve in space and the derivative of the function at any particular point represents the slope of the particular function at that point. For any function f(x) is said to be differentiable if the differentiation of the function exists and it is denoted by f'(x) or df(x)/dx. We also represent a function as, y = f(x) then
Derivative of a Function is represented as f'(x) or y’ or dy/dx
It is called the derivative of y with respect to x.
Derivative of a function is also define as the rate of change of the function with respect to any point on its domain.
First Principle of Differentiation
Suppose a function f(x) is defined in the neighborhood of ‘a’. If a and a + h belong to the domain of function f(x) then the differentiation of the function at x = a is given by,
f'(a) = lim x→a {f(x + h) – f(x)}/h
This is known as the first principle of differentiation. We use this first principle to find the derivative of the function at any given point and this derivative gives the slope of the function at that particular point.
Note: If the derivative of f(x) exists then the function f is said to be derivable or differentiable. Differentiation is the process of finding derivatives.
Geometrical Interpretation of Derivative of a Function
Consider the graph added below,

Function f(x) defined on an open interval (a, b). Let P be a point on the curve y = f(x). Let Q[(c – h), f(c – h)] and R be the point on either side of point P. Now,
Slope of chord PQ is, {f(c – h) – f(c)} / (-h)
Slope of chord PR can be written as, {f(c + h) – f(c)} / h
Now, we know that tangent to a curve at a point P is the limiting position of secant PQ when Q tends to P.
Similarly, it is also the limiting position of secant PR when R tends to P.
∴ h⇢ 0 points Q and R both tend to P from left and right hand sides.
∴ Slope of tangent at point P is,
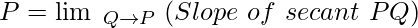
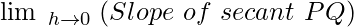
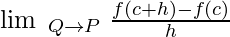
If these limits exist and are equal, there is a unique tangent at point P.
Slope of tangent is denoted by dy/dx i.e., f'(x)
Thus,
f'(x) = lim x→a {f(x + h) – f(x)}/h = lim x→a {f(x + h) – f(x)}/{-h}
How to Find Derivative of Function
To find the derivative of a function we use the first principle formula, i.e. for any given function f(x) whose derivative at x = a is to be found the first principle formula is,
f'(x) = lim x→a {f(x + h) – f(x)}/h
Simplifying the above we get the required derivative of the function at any point in the domain of the function.
Derivative of a Standard Functions
Derivative of some standard function are given below that are used to solve various problems of the differentiation. That includes,
Derivative of Constant Function
The constant functions are the functions whose value does not change with respect to the change in the value of the parameter of the function. They generally represent a straight line in the graph of the function. Derivative of the constant function is found as,
Let f(x) = k {where k is any constant}
∴ f(x + h) = k
Consider,
f'(x) = lim h→0 {f(x + h) – f(x)}/h
f'(x) = lim h→0 {k – k}/h = 0
f'(x) = 0
d(k)/dx = 0
Derivative of Exponential Function
Exponnetial Function are the function that are in the form of ex and the differentiation of the function is found using the first principle as,
Let f(x) = ex
f(x + h) = e(x+h)
f'(x) = lim h→0 {f(x + h) – f(x)}/h
f'(x) = lim h→0 {e(x+h) – ex}/h
f'(x) = lim h→0 ex{eh – 1}/h
f'(x) = ex
Derivative of Trigonometric Functions
Trigonometric functions are the function that uses trigonometric values and their differentiation is also easily found using the first principle concept as, suppose we have to find the differentiation of sin x then,
Let f(x) = sin x
f(x + h) = sin(x + h)
f'(x) = lim h→0 {f(x + h) – f(x)}/h
f'(x) = lim h→0 {sin (x + h) – sin (x)}/h
f'(x) = lim h→0 {2 cos (x + h + x)/2 . sin (x + h – x)/2}/h
f'(x) = lim h→0 {cos (2x + h)/2 . sin (h/2)}/(h/2)
f'(x) = lim h→0 {cos (2x + h)/2} . lim h/2→0 sin (h/2)/(h/2)
f'(x) = cos {(2x +0)/2}.1
f'(x) = cos (2x/2).1 = cos x
Thus, the derivative of sin x is cos x proved.
Similarly derivative of other trigonometric functions are added below,
- d(cos x)/dx = – sin x
- d(tan x)/dx = sec2 x
- d(cot x)/dx = – cosec2 x
- d(sec x)/dx = sec x . tan x
- d(cosec x)/dx = – cosec x . cot x
Derivative of Absolute Function
Absolute function is the function that gives the distance of point from origin. It is denoted using |x| and its derivative is calculated as,
d/dx(|x|) = x/|x|
where, x ≠ 0
Derivative of Logarithmic Function
Logarithimic Function are also called the log function and is represented as, log x and its derivative is found as,
d/dx (log x) = 1/x
Derivative of Inverse Function Formula
For any function f(x) its inverse is defined as f-1(x) and the derivative of the inverse function is found using the formula,
d/dx[f-1(x)] = 1/f'{f-1(x)}
Derivative of Implicit Function
Implict functions are the functions that can not be easily solve for y and their differention is called the Implict Differentiation. Derivative of Implict function is found using the chain rule.
Learn more about, Implicit Differentiation
Derivative of Composite Function
For any composite function h(x) such that, h(x) = f{g(x)}, to find the derivative of the composite function h(x) we first find the derivative of the composite function and then multiply the same with the derivative of g(x), i.e.
d/dx.f{g(x)} = f'(g(x)).g'(x)
Learn more about, Derivatives of Composite Functions
Algebra of Derivatives
We can also very easily perform algebra on the derivative of the functions. Suppose we are given with two differentiable function f(x) and g(x) then the rules of algebra state that,
- Sum of derivatives of the functions f and g is equal to the derivative of their sum, i.e.,
d/dx {f(x) + g(x)} = d/dx.f(x) + d/dx.g(x)
- Difference of derivatives of the functions f and g is equal to the derivative of their difference, i.e.,
d/dx {f(x) – g(x)} = d/dx.f(x) – d/dx.g(x)
- If we are given two function as the product then the derivative of the function is calculated as,
d/dx{f(x).g(x)} = f(x).d/dx{g(x)} + g(x).d/dx{f(x)}
This is also called the product rule in calculus.
- If we are given two function in quotient form then the derivative of the function is calculated as,
d/dx{f(x)/g(x)} = [f(x).d/dx{g(x)} – g(x).d/dx{f(x)}]/{g(x)}2
Various Derivative Formulas are,
- (d/dx) constant = 0
- (d/dx) xn = nxn-1
- d/dx) ex = ex
- (d/dx) ax = ax ln a
- (d/dx) ln x = (1/x)
Apart form these formulas some other derivative formulas are,
- (d/dx) [f(x) ± g(x)] = (d/dx) f(x) ± (d/dx) g(x)
- (d/dx) [f(x). g(x)] = f'(x). g(x) + f(x). g'(x)
- (d/dx) [f(x)/g(x)] = [f'(x). g(x) – f(x). g'(x)]/[g(x)]2
- (d/dx) [f(g(x))] = (d/dx) [f(g(x))] × (d/dx) [g(x)]
Learn more about, Derivative Formulas
Read More,
Examples on Derivative Rules
Example 1: Find the derivative of 3x + 4 using the first principle of derivative.
Solution:
Let f(x) = 3x + 4
f(x + h) = 3(x + h) + 4
Then,
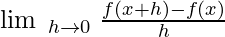
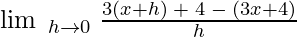
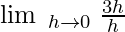
= 3
∴ f’ (x) = 3
Example 2: Find the derivative of
Using the First Principle of Derivative.
Solution:
Let f(x) = 1 / x2
f(x + h) = 1 / (x + h)2
Then,
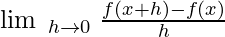
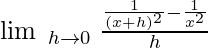
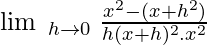
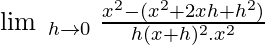
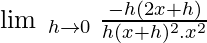
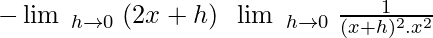
= -2x(1 / x2x2)
= -2 / x3
∴ f'(x) = -2 / x3
Let f(x) = x cos x
f(x + h) = (x + h) cos (x + h)
consider,
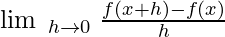
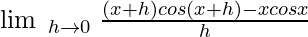
![Rendered by QuickLaTeX.com \lim\;_{h \to 0} \; \frac{x[cos (x + h) - cos x]+ h\;cos(x + h)}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10b385f03951f57ae88a70e1c463e794_l3.png)
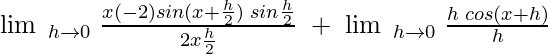
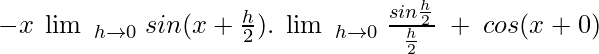
= -x sin x. 1 + cos x
= -x sin x + cos x
∴ f'(x) = -x sin x + cos x
Example 3: Differentiate the following functions,
- sin x / 1 + sin x
- ex / 1 + sin x
Solution:
we have
y = sin x / 1 + sin x
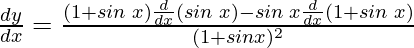
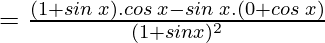
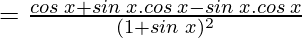
= cos x / (1 + sin x)2
y = ex / 1 + sin x
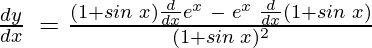
![Rendered by QuickLaTeX.com = \frac{e^x[1 + sin\;x - cos\;x]}{(1 + sin\;x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-020e18369075e423a8c1666a42502be4_l3.png)
Example 4: y = log 5(log7 x) find dy / dx
Solution:
Given,
Using logarithmic property, we can write,
y = log( log7x ) / log 5
![Rendered by QuickLaTeX.com \frac{dy}{dx} = \frac{1}{log\;5}.\frac{d}{dx}[log(log_7x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8016afd387b62c6f9c4a189c9be9b6a_l3.png)
= 1 / x log 5. log x
Example 5: If y = log(3x2 + 2x +1), find dy/dx
Solution:
y = log (3x2 + 2x +1)
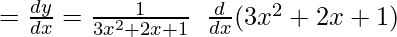
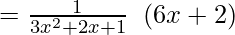
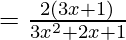
Example 6: Using First Principle find the derivative of √sin x
Solution:
Given,
f(x + h) = √sin (x + h)
f'(x) = limx→0 {f(x + h) – f(x)}/h
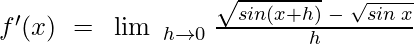
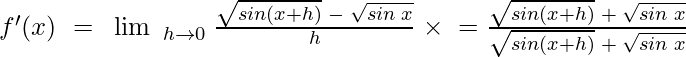
![Rendered by QuickLaTeX.com f'(x)~=~\;\lim\;_{h \to 0}\; \frac{sin(x + h) - sin\;x}{h[\sqrt{sin(x + h)} \;+\; \sqrt{sin\;x} ]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c6a17ed9f9533aafcca092d44ba1bb78_l3.png)
![Rendered by QuickLaTeX.com f'(x)~=~\lim\;_{h \to 0}\; \frac{2 cos\;(\frac{x + h+ x}{2})\;.\;sin\;(\frac{x + h - x}{2})}{h[\sqrt{sin(x + h)}\; +\;\sqrt{sin\;x} ]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a0fed88ad3cfa3b2d98a6b0f07b35fb_l3.png)
![Rendered by QuickLaTeX.com f'(x)~=~\lim\;_{h \to 0}\; \frac{2\;cos\;(x +\frac{h}{2})\;.\;sin(\frac{h}{2})}{h[\sqrt{sin(x + h)\;+\;\sqrt{sin\;x}}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74143a05acdc58a8d20547546adb8498_l3.png)
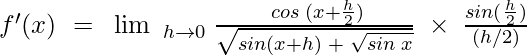
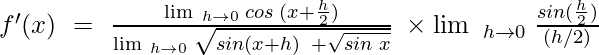
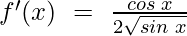
FAQs on Derivative of a Function
1. What is Derivative of a Function?
The derivative of a function is the rate of change of the function with respect to any value from the domain of the function. It gives the slope of the function at the given point.
2. What is Dervivative of Sin x?
The derivative of sin x is calculated as, suppose y = sin x, then
y'(x) = cos x
3. What is Derivative of Tan x?
The derivative of tan x is calculated as, suppose y = tan x, then
y'(x) = sec2 x
4. What is Derivative of Cos x?
The derivative of cos x is calculated as, suppose y = cos x, then
y'(x) = -sin x
5. What is Derivative of ex?
The derivative of ex is calculated as, suppose y = ex, then
y'(x) = ex
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...