Triangle Inequality Theorem, Proof & Applications

Triangle Inequality is the relation between the sides and angles of triangles which helps us understand the properties and solutions related to triangles. Triangles are the most fundamental geometric shape as we can’t make any closed shape with two or one side. Triangles consist of three sides, three angles, and three vertices.

The construction possibility of a triangle based on its side is given by the theorem named “Triangle Inequality Theorem.” The Triangle Inequality Theorem states the inequality relation between the triangle’s three sides. In this article, we will explore the Triangle Inequality Theorem and some of its applications as well as the other various inequalities related to the sides and angles of triangles.

In this article, we’ll delve into the concept of triangle inequality, the triangle inequality theorem, its significance, and its practical applications.

What is Triangle Inequality?

Triangle Inequality is a fundamental geometric principle that plays a vital role in various mathematical and real-world applications. It lays the foundation for understanding relationships between the sides of a triangle, contributing to fields such as geometry, physics, and computer science.

Triangle Inequality Theorem

Triangle Inequality Theorem states that “the sum of the length of any two sides of a triangle must be greater than the length of the third side.” If the sides of a triangle are a, b, and c then the Triangle Inequality Theorem can be represented mathematically as:

• a + b > c,
• b + c > a,
• c + a > b

Triangle Inequality Proof

In this section, we will learn the proof of the triangle inequality theorem. To prove the theorem, assume there is a triangle ABC in which side AB is produced to D and CD is joined.

Triangle Inequality Theorem Proof:

Notice that the side BA of Δ ABC has been produced to a point D such that AD = AC. Now, since ∠BCD > ∠BDC. 

By the properties mentioned above, we can conclude that BD > BC. 

We know that, BD = BA + AD

So, BA + AD > BC 

= BA + AC > BC 

So, this proved sum of two sides triangle is always greater than the other side.  

Let’s see an example based on Triangle Inequality Theorem to understand its concept more clearly.

Example: D is a point on side BC of triangle ABC such that AD = DC. Show that AB > BD. 

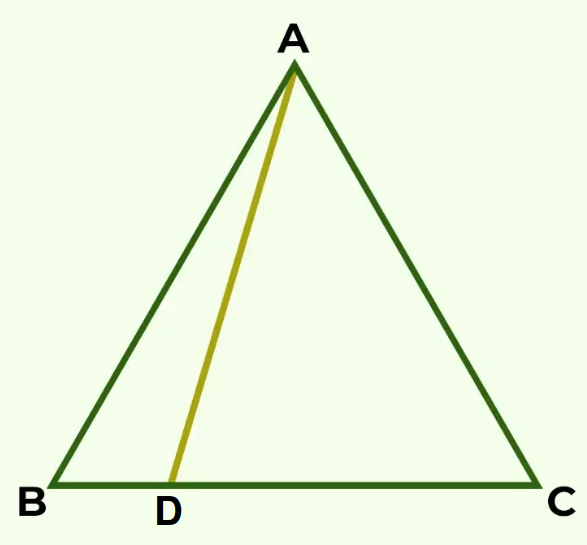
Solution:

In triangle DAC, 

AD = AC, 

∠ADC = ∠ACD (Angles opposite to equal sides)

∠ ADC is an exterior angle for ΔABD.

∠ ADC > ∠ ABD

⇒ ∠ ACB > ∠ ABC

⇒ AB > AC (Side opposite to larger angle in Δ ABC)

⇒ AB > AD (AD = AC)

Triangle Inequality Theorem – Applications & Uses

There are many applications in the geometry of the Triangle Inequality Theorem, some of those applications are as follows:

• To Identify the Triangles
• To Find the Range of Possible Values of the Sides of Triangles

How to Identify Triangles

To Identify the possibility of the construction of any given triangle with three sides, we can use the Triangle Inequality Theorem. If the given three sides satisfy the theorem, then the construction of this triangle is possible. 

For example, consider the sides of the triangle as 4 units, 5 units, and 7 units. 

As 4 + 5 > 7, 5 + 7 > 4, and 7 + 4 > 5. Thus, the triangle with sides 4 unit, 5 units, and 7 units is possible to construct.

Now take another example for not possible construction, consider the sides of the triangle to be 3 units, 4 units, and 9 units.

 As 3 + 4 [Tex]\ngtr        [/Tex] 9, therefore triangle with sides 3 units, 4 units and 9 units is not possible.

How to Find Range of Possible Values of Sides of Triangle

To find the range of possible values of the sides of a triangle when two sides are given as units and b units, you can follow these steps:

Step 1: Let’s assume the third side be x units.

Step 2: Now, using Triangle Inequality Theorem we know, 

a + b > x, a + x > b, and b + x > a

Step 3: Using all three conditions we can find the range for the third side.

Let’s consider an example for better understanding.

Example: Find the range for the third side of the triangle if the first two sides are 4 units and 7 units.

Solution:

Let’s assume the third side be x units.

Using Triangle Inequality Theorem, we get

4 + 7 = 11 > x, 4 + x > 7, and 7 + x > 4

Simplifying the above inequalities, we get

11 > x and x > 3.

Thus, possible range for the third sides is 3 < x < 11.

Various Inequalities in Triangle

If the a, b, and c are the sides of the triangle, then the following inequalities hold:

• [Tex]\frac{3}{2} \leq \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}<2 [/Tex]
• If angle C is obtuse (greater than 90°) then a²+b²<c²
• If C is acute (less than 90°) then a²+b²>c²
• [Tex] a b c \geq(a+b-c)(a-b+c)(-a+b+c) [/Tex]
• [Tex]a^2 b(a-b)+b^2 c(b-c)+c^2 a(c-a) \geq 0 [/Tex]
• For A.M., G.M., and H.M. we know that H.M. ≤ G.M. ≤ A.M. 

[Tex]\frac{3abc}{ab+bc+ac}\leq \sqrt[3]{abc} \leq \frac{a+b+c}{3} [/Tex]

If a, b, and c are sides of the triangle and A, B, and C are the interior angles opposite to those sides respectively then the following inequalities hold:

• [Tex]\cos A+\cos B+\cos C \leq \frac{3}{2} [/Tex]
• [Tex](1-\cos A)(1-\cos B)(1-\cos C) \geq \cos A \cdot \cos B \cdot \cos C [/Tex]
• [Tex]\sin A+\sin B+\sin C \leq \frac{3 \sqrt{3}}{2} [/Tex]
• [Tex]\sin ^2 A+\sin ^2 B+\sin ^2 C \leq \frac{9}{4} [/Tex]
• Using, A.M. G.M. inequality, [Tex]\sqrt[3]{\sin A \cdot \sin B \cdot \sin C} \leq \frac{\sin A+\sin B+\sin C}{3}        [/Tex], thus

[Tex]\sin A \cdot \sin B \cdot \sin C \leq\left(\frac{\sin A+\sin B+\sin C}{3}\right)^3 \leq\left(\sin \frac{A+B+C}{3}\right)^3=\sin ^3\left(\frac{\pi}{3}\right)=\frac{3 \sqrt{3}}{8} [/Tex]

• [Tex]\sin \frac{A}{2} \cdot \sin \frac{B}{2} \cdot \sin \frac{C}{2} \leq \frac{1}{8} [/Tex]
• [Tex]\tan ^2 \frac{A}{2}+\tan ^2 \frac{B}{2}+\tan ^2 \frac{C}{2} \geq 1 [/Tex]
• [Tex]\cot A+\cot B+\cot C \geq \sqrt{3}  [/Tex]
• [Tex]\sin A \cdot \cos B+\sin B \cdot \cos C+\sin C \cdot \cos A \leq \frac{3 \sqrt{3}}{4} [/Tex]

People Also View:

• Congruence of Triangles
• Angle Sum Property of Triangle
• Right Angled Triangle
• Properties of Triangle: Types of Triangles

Also Check : Triangles Class 9 NCERT Solutions

Sample Problems on Triangle Inequality

Problem 1: Determine whether the given set of side lengths can form a triangle according to the triangle inequality theorem.

a) 3, 4, 9

b) 5, 7, 12

c) 6, 10, 25

Solution:

For any triangle with sides a, b and c, using the triangle inequality theorem we get.

• a + b > c,
• b + c > a,
• c + a > b

We can use this to determine whether a triangle can be formed or not.

a) 3, 4, 9

As 3 + 4 < 9,

Thus, this triangle can’t be formed.

b) 5, 7, 12

As 5 + 7 = 12,

Thus, this triangle also can’t be formed.

c) 6, 10, 25

As 6 + 10 < 25,

Thus, this triangle also can’t be formed.

All the given triangles do not satisfy the triangle inequality theorem.

Problem 2: If the two sides of a triangle are 3 and 5. Find all the possible lengths of the third side.

Solution:

As we know, that for any triangle with sides a, b and c,

a – b < c < a + b

Let he unknown side be x,

Thus, 5 – 3 < x < 5 + 3

⇒ 2 < x < 8

Thus, third side can have any value between 2 and 8.

Practice Problem on Triangle Inequality

Problem 1: Given a triangle with sides of lengths 5 cm, 8 cm, and 12 cm, determine whether the triangle satisfies the triangle inequality theorem.

Problem 2: Suppose you have a triangle with sides of lengths 7 inches, 10 inches, and 28 inches. Can this triangle exist?

Problem 3: Three sticks have lengths 9 cm, 15 cm, and 20 cm. Can we form a triangle using these sticks?

Summary – Triangle Inequality Theorem, Proof & Applications

The Triangle Inequality Theorem is a foundational concept in geometry that elucidates the relationships between the lengths of the sides of a triangle. It asserts that the sum of the lengths of any two sides of a triangle must always exceed the length of the third side. This principle is mathematically articulated through the inequalities: a + b > c, b + c > a, and c + a > b, where a, b, and c represent the sides of the triangle. The proof of the theorem involves extending a side of a triangle and applying the properties of angles and sides to establish the inequality relation. The theorem not only facilitates the validation of the possibility of constructing a triangle given three lengths but also enables the determination of the range of possible values for the sides of a triangle. Its applications are vast and varied, including the identification of triangles, the determination of possible side lengths, and providing foundational knowledge that underpins further study in geometry, physics, and computer science. Through examples and proofs, the significance of the Triangle Inequality Theorem in both theoretical and practical contexts is made evident, showcasing its role in understanding and solving problems related to triangles.

FAQs on Triangle Inequality Theorem, Proof & Applications

What is the Triangle Inequality Theorem?

Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Can an Equilateral Triangle Violate the Triangle Inequality Theorem?

No, equilatral triangle can’t voilate the Triangle Inequality Theorem. As all sides in Equilateral Triangle are equal and sum of any two sides is twice the third i.e., greater than the third side.

What is the Converse of the Triangle Inequality Theorem?

Converse of the Triangle Inequality Theorem states that if sum of the lengths of any two sides of a triangle is greater than the length of third side, then given three sides can form a triangle.

What is the Triangle Inequality for Angles?

 The Triangle Inequality for Angles states that the sum of any two angles in a triangle must be greater than the measure of the third angle.

What is the Relationship between the Sides of a Right Triangle?

The relationship between the sides of a right-angle triangle is given by the Pythagoras Theorem. If the sides of right-angle triangle are a, b, and c (c is the greatest side) then by Pythagoras theorem:

a² + b² = c²