Maximum Score by travelling from (1, 1) to (N, N) on grid
Last Updated :
10 Apr, 2023
Given an integer N which corresponds to a N x N grid. The score you can get from a cell at the ith row and the jth column is i*j. You are initially at position (1, 1) of the grid and you have to reach (N, N) by making the score as max as possible. The only direction you can move is right (from (i, j) to (i, j + 1)) and down (from (i, j) to (i+1, j)). You are not allowed to go out of the grid. The answer might be a large number so return ans mod 10^9+7.
Examples:
Input: 3
Output: 22
Explanation: 1*1 + 1*2 + 2*2 + 2*3 + 3*3 = 22
Input: 10
Output: 715
Approach: To solve the problem follow the below idea:
You can visualize that the best path is in a zigzag fashion, i.e. from (1, 1) to (1, 2) to (2, 2) and so on. Thus, the answer would be the sum of the product of coordinates from
(1, 1) to (N, N)
(1*1)+(1*2)+(2*2)+…+(N*N)
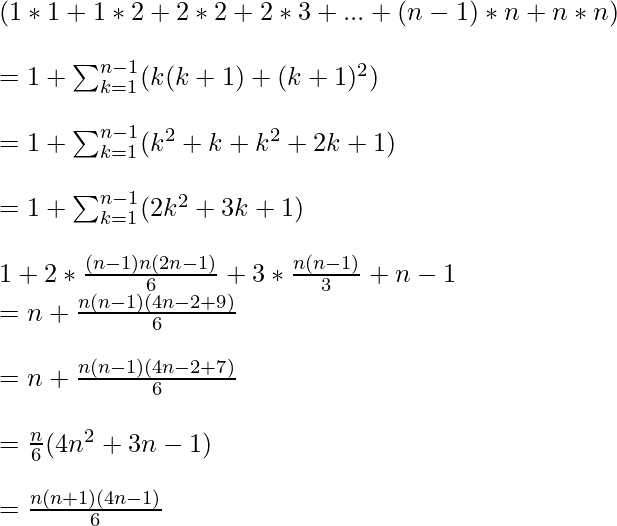
Illustration:
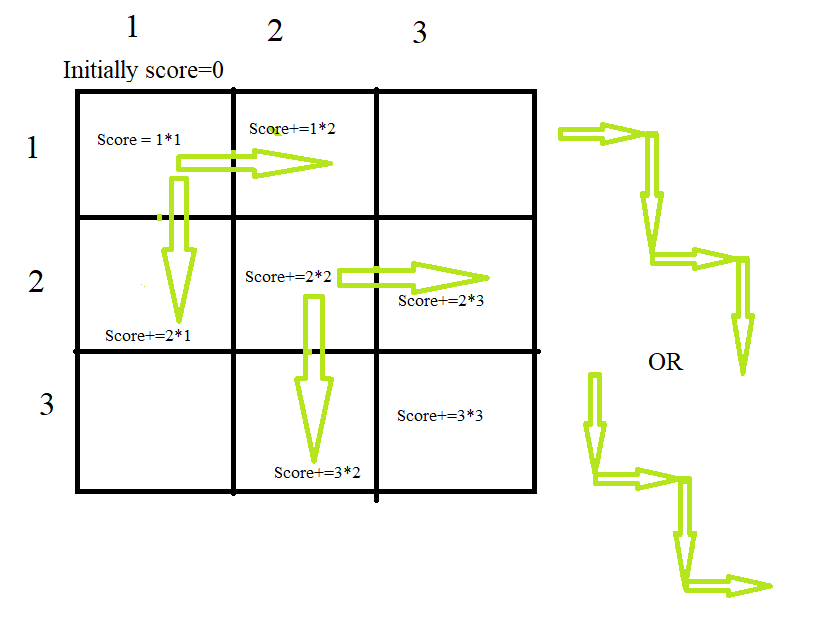
Best path for 1*1 to n*n is zigzag traversal
In the above illustration, we are given a 3*3 grid we need to find the best path which is shown in the figure. We have two paths which are best so we can choose any of them.
Below are the steps for the above approach:
- Initialize a variable ans that will store the final answer.
- Use the derived formula to find the answer.
- ans = (((((n * (n + 1)) % mod) * (4 * n – 1)) % mod) / 6) % mod.
- As the answer might be a large number so print ans as (ans % 10^9 + 7).
Below is the implementation for the above approach:
C++
// C++ code for the above approach:
#include <bits/stdc++.h>
const int mod = 1e9 + 7;
using namespace std;
void getScore(long long n)
{
long long ans
= (((((n * (n + 1)) % mod) * (4 * n - 1)) % mod)
/ 6)
% mod;
cout << ans << endl;
}
// Drivers code
int main()
{
getScore(2);
getScore(4);
getScore(10);
getScore(100);
}
Java
//Java code for the above approach:
import java.util.*;
public class Main {
final static int MOD = (int)1e9 + 7;
public static void getScore(long n) {
long ans = (((((n * (n + 1)) % MOD) * (4 * n - 1)) % MOD) / 6) % MOD;
System.out.println(ans);
}
// Drivers code
public static void main(String[] args) {
getScore(2);
getScore(4);
getScore(10);
getScore(100);
}
}
Python3
MOD = 10**9 + 7
def getScore(n):
ans = (((((n * (n + 1)) % MOD) * (4 * n - 1)) % MOD) // 6) % MOD
print(ans)
# Drivers code
getScore(2)
getScore(4)
getScore(10)
getScore(100)
C#
// C# code for the above approach:
using System;
public class GFG {
const int MOD = (int)1e9 + 7;
static void getScore(long n)
{
long ans
= (((((n * (n + 1)) % MOD) * (4 * n - 1)) % MOD)
/ 6)
% MOD;
Console.WriteLine(ans);
}
static public void Main()
{
// Code
getScore(2);
getScore(4);
getScore(10);
getScore(100);
}
}
// This code is contributed by lokesh.
Javascript
const MOD = 1e9 + 7;
function getScore(n) {
const ans = (((n * (n + 1)) % MOD) * ((4 * n) - 1) % MOD) / 6 % MOD;
console.log(ans);
}
// Driver code
getScore(2);
getScore(4);
getScore(10);
getScore(100);
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...