Prove that Medians of a Triangle are Concurrent

Concurrent lines are line segments, two or more, crossing through a single point of intersection. The point is called the point of concurrency. The point of concurrency is clearly visible in the case of triangles. These lines in the case of triangles are the altitudes, medians as well as perpendicular bisectors. 

There are many lines of concurrency in the triangle which are discussed in this article.

Medians of Triangle 

The line segment inside the triangle connects the vertex, to the side opposite to that vertex in the triangle. This line segment is known as the median. PS is the median in triangle QPR, where the bottom line segment, RS can be divided into two equal parts where QR = QS. The three medians of the triangle intersect at a point known as the centroid. 

Altitudes of Triangle

The altitudes of a triangle emerge from each of the vertexes of the triangle and intersect each other at a single point known as the orthocenter. 

Angle Bisectors

The line segments bisecting the angles from each of the vertices of the triangle are known as angle bisectors. There is a point of intersection for the angle bisectors, known as the incenter. 

Perpendicular Bisectors 

The line segments intersect the opposite sides of the triangle at right angles. These line segments go through a common point, which is known as the circumcenter. 

Properties of Median of Triangle

• The median of a triangle divides the triangle into two sub-triangles each of an equivalent area. 
• The three medians of the triangle always intersect at a single point, irrespective of the type of triangle. 
• The line segment which is bisected by the median is divided into two equivalent parts.
• A median arises from each of the vertices of the triangle. 
• There can be a total of 6 triangles, which can be derived from three medians of a triangle. 
• All the medians of a triangle meet at a point known as the centroid. 

Concurrency of Medians of a Triangle

Proof: A triangle ABC with the median being AE, BD, and CF respectively. F is the midpoint of the line segment AB, D of AC, and E of BC respectively. 

Now, triangles ABC and DEC are similar in nature. 

AC = 2CD ; ∠ ACB = ∠ DCE; BC = 2CE (SAS similarity) …… (I)

Also, DE//AB, due to the similarity of the triangles ACE and EDC respectively. 

Similarly, the following three pairs of angles are equivalent ; 

∠ GED = ∠ GAB 

∠ GDE = ∠ GBA

∠ DGE = ∠ AGB

Therefore, the triangles, ABG and EDG are similar in nature (AAA similarity)

Hence, 

DE/AB = GE/GA = 1/2 

GE = 1/2GA

GE = 1/3 AE ….(II)

Also, 

GD = 1/2 GB

GD = 1/3 BD … (III)

The same procedure can be repeated for the line segment AE in combination with CE, and the pair BD with CE. This implies that each of the above pair of points divides the median into two segments. This point is the one and only point in the triangle known as the centroid of the triangle, G. 

Solved Examples on Medians of Triangle

Example 1: Find if the lines 4x – 6y + 10 = 0, 6x + 8y – 14 = 0 and 18x – 10y + 16 =0 are concurrent.

Solution: 

The three lines are:

4x – 6y + 10 = 0

6x + 8y – 14 = 0

18x – 10y + 16 =0

Now, as per the condition of the concurrence of lines, we need to find the determinant of the coefficients.

Hence,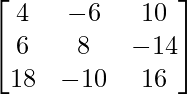

= 4(128 – 140) – (–6)(96 + 252) + 10(–60 – 144)

= 4(–12) + 6(348) + 10(– 204)

= – 48 + 2088 – 2040

= 0

Therefore, the given three lines are concurrent.

Example 2: In triangle ABC, consider, that G is the centroid and BC = 20 units. What is the length of the line segment BD?

Solution:

Here, AD is the median of the triangle ABC, therefore, D is the midpoint of the line segment BC

AD, CE, and BF are the medians of the triangle 

Now, BD = DC = 1/2 BC

So, 

BC = 20 units

Therefore, BD = 1/2 × 20 = 10 units

Example 3: Assume that the two angles of a triangle are 35° and 65° respectively thus calculating the third angle of the triangle.

Solution:

Assume the angles of the triangle to be ∠A, ∠B, and ∠C

Here we are going to find ∠C

We have ∠A = 35° ∠B = 65°

As we know that the property of the triangle (angle sum property) 

∠A + ∠B + ∠C = 180°

∠C = 180° – ∠A – ∠B

∠C = 180° – 35° – 65°

∠C = 80°

Hence,

The third angle of the triangle is 80°.

Example 4:  Assume that △XYZ ~ △PQR, XY = 6 m, YZ = 10 m, XZ = 12 m, PQ = 12 m and QR = 20 m, Find PR.

Solution: 

Here we have,

 ΔXYZ ~ ΔPQR, 

Further, According to the property of triangles (similar triangles have proportional sides)

XY/PQ = YZ/QR = XZ/PR  

6/12 = 10/20 = 12/PR

1/2 = 1/2 =  12/PR

PR = 24 m

Therefore, the length of PR is 24 m. 

FAQs on Medians of Triangle

Question 1: Difference between Concurrent Lines and Intersecting Lines?

Answer:

Concurrent lines:

• At least three line segments pass through a single point.
• The point of intersection is known as the point of concurrency.

Intersecting lines:

• At least two line segments cross each other. 
• The point of intersection is known as the point of intersection. 

Question 2: What is a centroid?

Answer:

The centroid of any geometrical figure is the arithmetic mean position of all the points in the figure. 

Question 3: Define orthocenter. 

Answer:

The point at which all the altitudes of a triangle coincide is called the orthocenter of the triangle.

Question 4: Can the centroid and orthocenter be the same?

Answer:

Yes, for an equilateral triangle centroid and orthocenter are the same.

Related Resource

• Area of a Triangles
• Types of Angles
• Measurement of Angle