What are the six trigonometry functions?

Trigonometry can be defined as the branch of mathematics that determines and studies the relationships between the sides of a triangle and angles subtended by them. Trigonometry is basically used in the case of right-angled triangles. Trigonometric functions define the relationships between the 3 sides and the angles of a triangle. There are 6 trigonometric functions mainly. Before going into the study of the trigonometric functions we will learn about the 3 sides of a right-angled triangle.

The three sides of a right-angled triangle are as follows,

• Base The side on which the angle θ lies is known as the base.
• Perpendicular It is the side opposite to the angle θ  in consideration.
• Hypotenuse It is the longest side in a right-angled triangle and opposite to the 90° angle.

Trigonometric Functions

Trigonometry has 6 basic trigonometric functions, they are sine, cosine, tangent, cosecant, secant, and cotangent. Now let’s look into the trigonometric functions. The six trigonometric functions are as follows,

• sine It is represented as sin θ and is defined as the ratio of perpendicular and hypotenuse.
• cosine It is represented as cos θ and is defined as the ratio of base and hypotenuse.
• tangent It is represented as tan θ and is defined as the ratio of sine and cosine of an angle. Thus the definition of tangent comes out to be the ratio of perpendicular and base.
• cosecant It is the reciprocal of sin θ and is represented as cosec θ.
• secant It is the reciprocal of cos θ and is represented as sec θ.
• cotangent It is the reciprocal of tan θ and is represented as cot θ.

What are the six trigonometry functions?

The six trigonometric functions have formulae for the right-angled triangles, the formulae help in identifying the lengths of the sides of a right-angled triangle, lets take a look at all those formulae,

Trigonometric Functions	Formulae
sin θ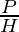
cos θ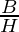
tan θ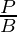
cosec θ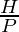
sec θ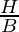
cot θ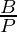

The below table shows the values of these functions at some standard angles,

Function	0°	30°	45°	60°	90°
					∞
	∞
					∞
	∞

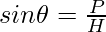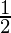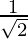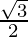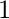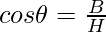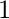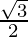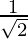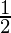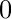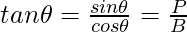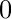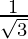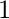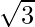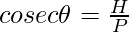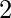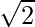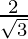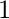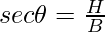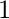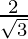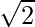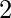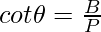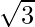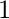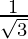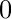Note: It is advised to remember the first 3 trigonometric functions and their values at these standard angles for ease of calculations.

Sample Problems

Question 1: Evaluate sine, cosine, and tangent in the following figure.

Solution: 

Given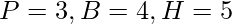 

Using the trigonometric formulas for sine, cosine and tangent,

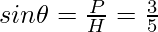
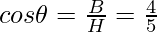
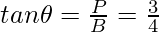
Question 2: In the same triangle evaluate secant, cosecant, and cotangent. 

Solution: 

As it is known the values of sine, cosine and tangent, we can easily calculate the required ratios.

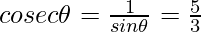
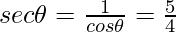
Question 3: Given 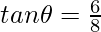, evaluate sin θ.cos θ.

Solution: 

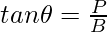
Thus P=6, B=8

Using Pythagoras theorem,

H²=P²+B²

H²=36+64=100

Therefore, H =10

Now,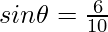 

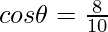
Question 4: If 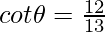, evaluate tan²θ.

Solution: 

Given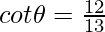 

Thus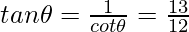 

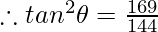
Question 5: In the given triangle, verify sin²θ+cos²θ = 1

Solution: 

Given P=12, B=5, H=13

Thus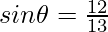 

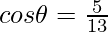
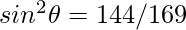
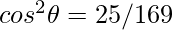
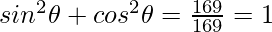
Hence verified.