Class 11 RD Sharma Solutions – Chapter 5 Trigonometric Functions – Exercise 5.1 | Set 1
Last Updated :
21 Feb, 2021
Prove the following identities (1 – 13)
Question 1. sec4θ – sec2θ = tan4θ + tan2θ
Solution:
We have
sec4θ – sec2θ = tan4θ + tan2θ
Taking LHS
= sec4θ – sec2θ
= sec2θ(sec2θ – 1)
Using sec2 θ = tan2θ + 1, we get
= (1 + tan2θ)tan2θ
= tan2θ + tan4θ
Hence, LHS = RHS (Proved)
Question 2. sin6θ + cos6θ = 1 – 3sin2θcos2θ
Solution:
We have
sin6θ + cos6θ = 1 – 3sin2θcos2θ
Taking LHS
= sin6θ + cos6θ
= (sin2θ)3 + (cos2θ)3
Using a3 + b3 = (a + b)(a2 + b2 – ab), we get
= (sin2θ + cos2θ)(sin4θ + cos4θ – sin2θcos2θ)
Using a2 + b2 = (a + b)2 – 2ab and sin2θ + cos2θ = 1, we get
= (1)[(sin2θ + cos2θ)2 – 2sin2θcos2θ – sin2θcos2θ]
= (1)[(1)2 – 3sin2θcos2θ]
= 1 – 3sin2θcos2θ
Hence, LHS = RHS (Proved)
Question 3. (cosecθ – sinθ)(secθ – cosθ)(tanθ + cotθ) = 1
Solution:
We have
(cosecθ – sinθ)(secθ – cosθ)(tanθ + cotθ) = 1
Taking LHS
= (cosecθ – sinθ)(secθ – cosθ)(tanθ + cotθ)
Using cosecθ = 1/sinθ and secθ = 1/cosθ
= 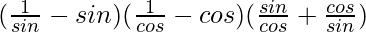
= 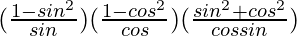
= 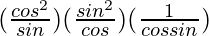
= 1
Hence, LHS = RHS (Proved)
Question 4. cosecθ(secθ – 1) – cotθ(1 – cosθ) = tanθ – sinθ
Solution:
We have
cosecθ(secθ – 1) – cotθ(1 – cosθ) = tanθ – sinθ
Taking LHS
= 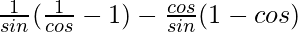
= 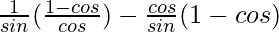
= ![Rendered by QuickLaTeX.com \frac{(1-cosθ)}{sinθ}[(\frac{1}{cosθ})-cosθ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-17fdea849a6df666a15b02eff54bd61c_l3.png)
= 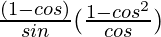
= 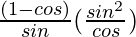
= 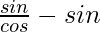
= 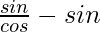
Hence, LHS = RHS(Proved)
Question 5. 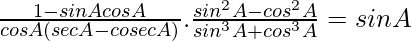
Solution:
We have
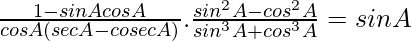
Taking LHS
= 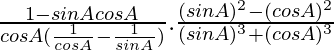
Using a2 – b2 = (a + b)(a – b) and a3 + b3 = (a + b)(a2 + b2ab), we get
= 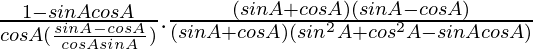
= 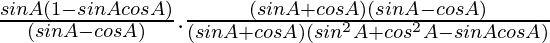
= 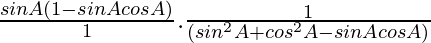
= 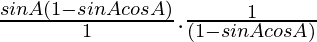
= sinA
Hence, LHS = RHS(Proved)
Question 6. 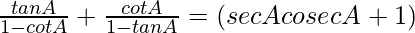
Solution:
We have
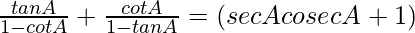
Taking LHS
= 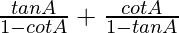
Using tanA = sinA/cosA and cotA = cosA/sinA, we get
= 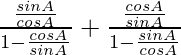
= 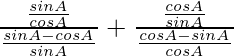
= 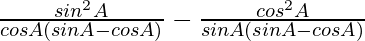
= 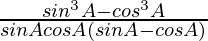
Using a3 – b3 = (a – b)(a2 + b2 + ab), we get
= ![Rendered by QuickLaTeX.com \frac{(sinA-cosA)[(sinA)^2+(cosA)^2+sinAcosA]}{sinAcosA(sinA-cosA)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8c01289874bece060d07faa482934ca_l3.png)
= 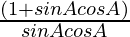
= 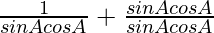
Using cosecA = 1/sinA and secA = 1/cosA, we get
= secAcosecA + 1
Hence, LHS = RHS(Proved)
Question 7.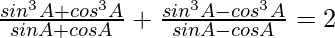
Solution:
We have
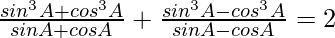
Taking LHS
= 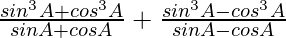
Using a3 ± b3 = (a ± b)(a2 + b2 ± ab), we get
= 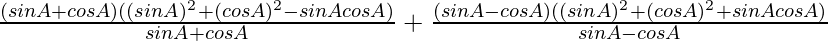
Using sin2θ + cos2θ = 1, we get
= 1 – sinAcosA + 1 + sinAcosA
= 2
Hence, LHS = RHS(Proved)
Question 8. (secAsecB + tanAtanB)2 – (secAtanB + tanAsecB)2 = 1
Solution:
We have
(secAsecB + tanAtanB)2 – (secAtanB + tanAsecB)2 = 1
Taking LHS
= (secAsecB + tanAtanB)2 – (secAtanB + tanAsecB)2
Expanding the above equation using the formula
(a + b)2 = a2 + b2 + 2ab
= (secAsecB)2 + (tanAtanB)2 + 2(secAsecB)(tanAtanB) –
(secAtanB)2 – (tanAsecB)2 – 2(secAtanB)(tanAsecB)
= sec2Asec2B + tan2Atan2B – sec2Atan2B – tan2Asec2B
= sec2A(sec2B – tan2B) – tan2A(sec2B – tan2B)
= sec2A – tan2A -(Using sec2θ – tan2θ = 1)
= 1
Hence, LHS = RHS(Proved)
Question 9. 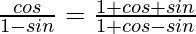
Solution:
We have
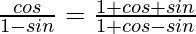
Taking RHS
= 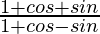
= 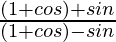
= 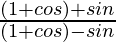 ×
×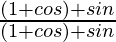
= 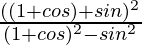
= 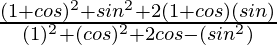
= 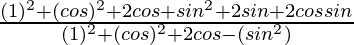
= 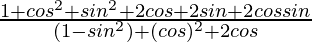
= 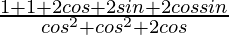
= 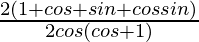
= 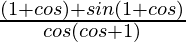
= 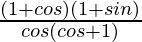
= 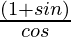
= 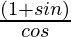 ×
×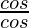
= 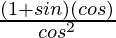
= 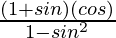
= 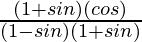
= 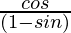
Hence, RHS = LHS(Proved)
Question 10. 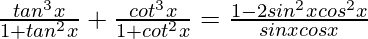
Solution:
We have
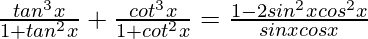
Taking LHS
= 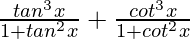
Using 1 + tan2x = sec2x and 1 + cot2x = cosec2x, we get
= 
= 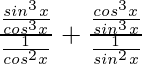
= 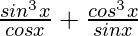
= 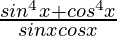
= 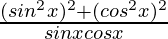
Using a2 + b2 = (a + b)2 – 2ab, we get
= 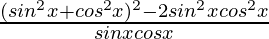
= 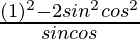
= 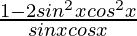
Hence, LHS = RHS (Proved)
Question 11. 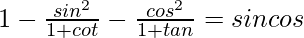
Solution:
We have
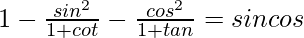
Taking LHS
= 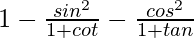
By using the formulas cotθ = cosθ/sinθ and tanθ = sinθ/cosθ, we get
= 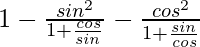
= 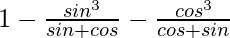
= 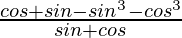
Using a3+b3 = (a + b)(a2 + b2 – ab), we get
= 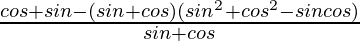
= 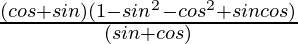
= 1 – (sin2θ + cos2θ) + sinθcosθ
= 1 – 1 + sinθcosθ
= sinθcosθ
Hence, LHS = RHS (Proved)
Question 12.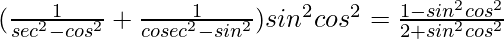
Solution:
We have
= 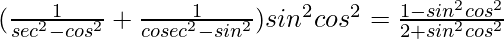
Taking LHS
= 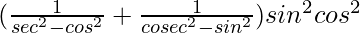
= 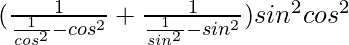
= 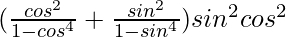
= 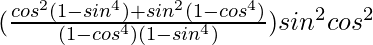
= 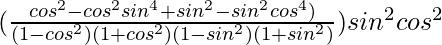
= 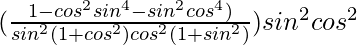
= 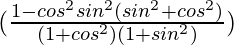
= 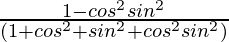
= 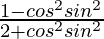
Hence, LHS = RHS(Proved)
Question 13. (1 + tanαtanβ)2 + (tanα – tanβ)2 = sec2αsec2β
Solution:
We have
(1 + tanαtanβ)2 + (tanα – tanβ)2 = sec^2αsec2β
Taking LHS
= (1 + tanαtanβ)2 + (tanα – tanβ)2
= (1 + tan2αtan2β + 2tanαtanβ) + (tan2α + tan2β – 2tanαtanβ)
= 1 + tan2αtan2β + tan2α + tan2β
= (1 + tan2β) + tan2α(1 + tan2β)
= (1 + tan2β)(1 + tan2α)
= sec2αsec2β
Hence, LHS = RHS (Proved)
Share your thoughts in the comments
Please Login to comment...