Interpolation Formula

Last Updated : 01 May, 2024

Interpolation formula is a method to find new values of any function using the set of available values through interpolation. It is an important statistical tool used to calculate the value between two points on the curve of a function from the given points which also lie on the same curve.

In statistical analysis and interpretation, sometimes it is found that a given series happens to be incomplete rather than complete, i.e., some values in the series remain unknown. But to derive correct results, it becomes essential to find the missing or unknown values in the series. The statistical technique that is used to estimate the unknown values on the basis of available data is called interpolation.

What Is Interpolation?

Interpolation is the process of calculating a value between two points on the curve of a function from the given points which also lie on the same curve. In other words, interpolation involves the calculation of new values from the already available set of values. Using interpolation, the diverse data can be converted into a concise function, such that each point in the data passes through the curve of such function. It is generally used in geography to predict data points such as noise level, rainfall, elevation, and so on.

Interpolation Formula

There are various formulae used to find the Interpolation and some of them are,

Linear Interpolation Formula
Lagrange Interpolation Formula
Leading Difference Formula
Quadratic Interpolation Formula

Linear Interpolation Formula

This method is used where the given data set does not consist of more than two ordered pairs. The value of the function at a certain value of the abscissa is obtained using the given ordered pairs.

$f(x) = f(x_0) + (x − x_0) \dfrac{f(x_1) − f(x_0)}{x_1 − x_0}$

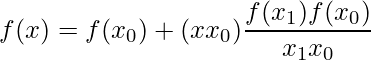
or

$y = y_0 + (x - x_0) \dfrac{y_1 - y_0}{x_1 - x_0}$

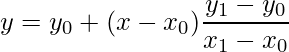
Lagrange Interpolation Formula

This method is employed where the given data set consists of more than two ordered pairs and can be used to derive a polynomial, which further assumes certain arbitrary values on certain points.

$f(x) = \dfrac{(x − x_0)(x-x_2)(x-x_3)(x-x_4)}{(x_1 − x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)} + \dfrac{(x − x_0)(x − x_1)(x − x_3)(x − x_4)}{(x_2 − x_0)(x_2 − x_1)(x_2 − x_3)(x_2 − x_4)}+\dfrac{(x − x_0)(x − x_1)(x − x_2)(x − x_4)}{(x_3 − x_0)(x_3 − x_1)(x_3 − x_2)(x_3 − x_4)}+....$

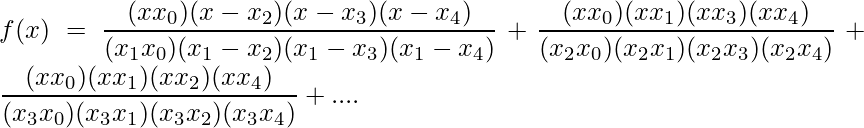
Leading Difference Formula

This method is used when the data set itself is kind of incomplete, i.e., where the frequency of one or more data sets is missing. In this case, the leading difference up to the number of known items is always zero and is given as:

△ⁿ₀ = (y − 1)ⁿ = yⁿ − ay^n-1+ by^n-2 − cy^n-3 +….+ y⁰ = 0

Quadratic Interpolation Formula

It is a refined form of linear interpolation method and is given as:

$f(x_j + θh) ≈ f_j + θΔf_j + \frac{1}{2}θ(θ-1)Δ^2f_j$

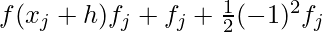
Interpolation Formula for unequal intervals

In numerical analysis, interpolation formulas are used to estimate values between known data points. For unequal intervals, one common method is the Lagrange Interpolation. This technique is especially useful when the intervals between your data points vary, as it doesn’t require the intervals to be equal.

$P(x) = \sum_{i=0}^{n} y_i \ell_i(x) \quad \text{where} \quad \ell_i(x) = \prod_{\substack{j=0 \\ j \neq i}}^{n} \frac{x - x_j}{x_i - x_j}$

Key Points

P(x): This is the polynomial that interpolates the points.

∑∑: The summation symbol, aggregating contributions from each term indexed by 𝑖i.

𝑦𝑖yi: The function values at each 𝑥𝑖xi.

ℓ𝑖(𝑥)ℓi(x): The Lagrange basis polynomial for each point 𝑥𝑖xi, which is crucial for ensuring that 𝑃(𝑥)P(x) passes through each data point exactly.

∏∏: The product symbol, representing the multiplication across all terms except when 𝑗=𝑖j=i.

𝑥−𝑥𝑗𝑥𝑖−𝑥𝑗xi−xjx−xj: The individual terms of the product that construct each basis polynomial ℓ𝑖(𝑥)ℓi(x), ensuring it equals 1 at 𝑥𝑖xi and 0 at all other 𝑥𝑗xj.

Interpolation Formula for equal intervals

The interpolation formula for equal intervals, often used in methods like Newton’s divided differences or polynomial interpolation, can be expressed in LaTeX as follows:

$P(x) = f(x_0) + \Delta x f[x_0, x_1] \cdot (x - x_0) + \Delta x^2 f[x_0, x_1, x_2] \cdot (x - x_0)(x - x_1) + \ldots$

Uses of Interpolation

Various uses of Interpolation are given below,

Deriving a Function From a Data Set

The diverse and scattered data points can be turned into a compact function using interpolation so that each point in the data travels through the curve of such a function. This makes it so much easier to understand the whole data in just one glance. Data can be converted into the following form:

p(x) = a₀ + a₁e^x + a₂e^2x +…..+ a_ne^nx

Obtaining Piecewise Polynomials

With the help of interpolation, one can also approximate functions into polynomials, i.e., simpler forms, which would make it easier to integrate and differentiate such functions to facilitate the calculations pertaining to areas under curves.

Many a time, the problems involving integration are very difficult to be solved analytically. In such cases, interpolation is used to alter the integrands and polynomials to make calculations easier.

Difference Between Interpolation and Extrapolation

The difference between Interpolation and Extrapolation are discussed in the table given below,

Interpolation	Extrapolation
It is the process of calculating a value between two points on the curve of a function from the given points which also lie on the same curve.	It is the way of predicting the magnitude of the reliant factor for an individual entity that is beyond the scope of the dataset.
As the name suggests, “inter”-polation works within the scope of the given data.	Extrapolation works outside the scope of the given data.

Read More

Solved Examples on Interpolation Formula

Example 1: Interpolate the value of y at x = 3, if two of the ordered pairs are (−5, 5), (5, 7).

Solution:

Given

x = 3, x₀ = −5, x₁ = 5, y₀ = 5, y₁ = 7

Since, 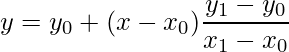$y = y_0 + (x - x_0) \dfrac{y_1 - y_0}{x_1 - x_0}$

$y = 5 + (3 − (−5)) \dfrac{7 − 5}{5 − (-5)}$

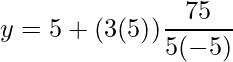
= 5 + 8(.2)

=5 + 1.6

y = 6.6

Example 2: Interpolate the missing value in the following table:

X	Y
1990	100
1991	107
1992	?
1993	157
1994	212

Solution:

Since the known values of Y are 4, the fourth leading difference will be zero. Thus,

△⁴₀ = (y − 1)⁴ = y⁴ − 4y³ + 6y² − 4y¹ + y⁰ = 0

Substituting the values of y’s we have,

212 − 4(157) + 6y₂ − 4y₁ + y₀ = 0

6y₂ = 628 − 212 + 428 − 100

y₂ = 124

Examples 3: The table below depicts insurance premiums payable to different age groups. Find the premium payable at 17.

Age	Premium Payable
15	11.1
25	12.6
35	14.3
45	16.1
55	18.3

Solution:

Age Premium(Y) △¹ △² △³ △⁴
15 = x₀ 11.1 = y₀
+1.5 = △¹₀
25 = x₁ 12.6 = y₁ +0.2 = △²₀
+1.7 = △¹₁ −0.1 = △³₀
35 = x₂ 14.3 = y₂ +0.1 = △²₁ +0.4 = △⁴₀
+1.8 = △¹₃ +0.3 = △³₁
45 = x₃ 16.1 = y₃ +0.4 = △²₂
+2.2 = △¹₄
55 = x₄ 18.3 = y₄
Now, x = 17 – 15/25 – 15 = 2/10 = 0.2

Hence, Y₁₇ = 11.1 + 0.3 − 0.016 − 0.0048 − 0.0134 = 11.4

Thus premium payable at 17 is 11.4

Example 4: Find the value of y when x = 5 from the following data:

x	y
2	1
3	5
4	13
6	61
7	125

Solution:

Applying Lagrange Formula,

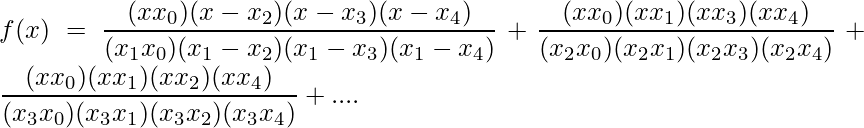
$f(x) = 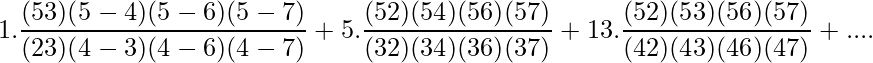\dfrac{(x − x_0)(x-x_2)(x-x_3)(x-x_4)}{(x_1 − x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)} + \dfrac{(x − x_0)(x − x_1)(x − x_3)(x − x_4)}{(x_2 − x_0)(x_2 − x_1)(x_2 − x_3)(x_2 − x_4)}+\dfrac{(x − x_0)(x − x_1)(x − x_2)(x − x_4)}{(x_3 − x_0)(x_3 − x_1)(x_3 − x_2)(x_3 − x_4)}+....$

f(x) = $1.\dfrac{(5−3)(5-4)(5-6)(5-7)}{(2−3)(4-3)(4-6)(4-7)}+5.\dfrac{(5−2)(5−4)(5−6)(5−7)}{(3−2)(3−4)(3−6)(3−7)}+13.\dfrac{(5−2)(5−3)(5−6)(5−7)}{(4−2)(4−3)(4−6)(4−7)}+....$

= 0.1 − 2.5 + 1.3 + 30.5 − 12.5

= 28.6

Example 5: Reconstruct the following data with the class intervals halved using interpolation:

Marks	Number of Students
0 – 10	50
10 – 20	65
20 – 30	85

Solution:

For estimating the marks in the class interval 0-5, 10-15, and 20-25, we will have to interpolate the values of less than 5, less than 15 and less than 25 respectively.

Interpolation of less than 5

x = 5−10/10 = −0.5

y₅ = y0 + x.△10 + [x(x−1).△²]/2 = 25

Similarly,

Interpolation of less than 15 = 80

Interpolation of less than 25 = 155

Thus, the reconstructed table is as follows:

Marks Cumulative Frequency Marks Number of Students
Less than 5 25 0 – 5 22
Less than 10 50 5 – 10 25
Less than 15 80 10 – 15 30
Less than 20 115 15 – 20 35
Less than 25 155 20 – 25 40
Less than 30 200 25 – 30 45

Marks	Cumulative Frequency	Marks	Number of Students
Less than 5	25	0 – 5	22
Less than 10	50	5 – 10	25
Less than 15	80	10 – 15	30
Less than 20	115	15 – 20	35
Less than 25	155	20 – 25	40
Less than 30	200	25 – 30	45

Interpolation Formula – FAQs

What is Interpolation?

Interpolation is an important statistical tool. It is the process of calculating a value between two points on the curve of a function from the given points which also lie on the same curve.

Why is Interpolation Important?

Interpolation is needed to compute the value of a function for an intermediate value of the independent function.

What are Piecewise Polynomials?

Approximated functions converted into polynomials, i.e., simpler forms, which would to make it easier to integrate and differentiate such functions to facilitate the calculations pertaining to areas under curves are called piecewise polynomials

What are the Various Methods of Interpolation?

The various methods of interpolation are,

Linear Interpolation Formula
Nearest Neighbor Method
Quadratic Interpolation
Lagrange Formula
Newton Formula

What is the Use of Interpolation?

Deriving a Function From a Data Set: The diverse and scattered data points can be turned into a compact function using interpolation, so that each point in the data travels through the curve of such function. This makes it so much easier to understand the whole data in just one glance. Data can be converted into the following form:

p(x) = a₀ + a₁e^x + a₂e^2x +…..+ a_ne^nx

What is the Difference between Interpolation and Extrapolation?

Interpolation is the process of calculating a value between two points on the curve of a function from the given points which also lie on the same curve, whereas extrapolation is the way of predicting the magnitude of the reliant factor for an individual entity that is beyond the scope of the dataset.

Suggest improvement

Linear Interpolation Formula

Share your thoughts in the comments

Age	Premium(Y)	△¹	△²	△³	△⁴
15 = x₀	11.1 = y₀
		+1.5 = △¹₀
25 = x₁	12.6 = y₁		+0.2 = △²₀
		+1.7 = △¹₁		−0.1 = △³₀
35 = x₂	14.3 = y₂		+0.1 = △²₁		+0.4 = △⁴₀
		+1.8 = △¹₃		+0.3 = △³₁
45 = x₃	16.1 = y₃		+0.4 = △²₂
		+2.2 = △¹₄
55 = x₄	18.3 = y₄

Interpolation Formula

What Is Interpolation?

Interpolation Formula

Linear Interpolation Formula

Lagrange Interpolation Formula

Leading Difference Formula

Quadratic Interpolation Formula

Interpolation Formula for unequal intervals

Interpolation Formula for equal intervals

Uses of Interpolation

Deriving a Function From a Data Set

Obtaining Piecewise Polynomials

Difference Between Interpolation and Extrapolation

Solved Examples on Interpolation Formula

Interpolation Formula – FAQs

What is Interpolation?

Why is Interpolation Important?

What are Piecewise Polynomials?

What are the Various Methods of Interpolation?

What is the Use of Interpolation?

What is the Difference between Interpolation and Extrapolation?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?